下表显示出函数值 随自变量
随自变量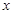 变化的一组数据,由此可判断它最可能的函数模型为
变化的一组数据,由此可判断它最可能的函数模型为
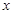 |
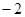 |
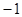 |
0 |
1 |
2 |
3 |
 |
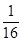 |
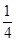 |
1 |
4 |
16 |
64 |
( )
A.一次函数模型 B.二次函数模型 C.指数函数模型 D.对数函数模型
某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为(1);在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为(2).
则完成(1)(2)这两项调查宜采用的抽样方法依次是( )
| A.分层抽样法,系统抽样法 |
| B.分层抽样法,简单随机抽样法 |
| C.系统抽样法,分层抽样法 |
| D.简单随机抽样法,分层抽样法 |
观察新生婴儿的体重表,其频率分布直方图如图2-1所示,则新生婴儿体重在[2 700,3 000)的频率为( )
图2-1
| A.0.001 | B.0.1 | C.0.2 | D.0.3 |
为了考察两个变量x和y之间的线性相关性,甲、乙两个同学各自独立地做了10次试验和15次试验,并且利用线性回归方法,求得回归直线分别为l1和l2,已知两个人在试验中发现对变量x的观测数据的平均数都为s,对变量y的观测数据平均数都为t,那么下列说法正确的是( )
| A.l1和l2有交点(s,t) | B.l1和l2相交,但交点不一定是(s,t) |
| C.l1和l2必平行 | D.l1和l2必重合 |
某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用图2-2-17中的条形图表示.根据条形图可得这50名学生这一天平均每人的课外阅读时间为…( )
图2-2-17
| A.0.6小时 | B.0.9小时 |
| C.1.0小时 | D.1.5小时 |
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如图2-2-16,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a,b的值分别为( )
图2-2-16
| A.0.27,78 | B.0.27,83 |
| C.2.7,78 | D.2.7,83 |