如图所示，边长为L的正方形线圈abcd与阻值为R的电阻组成闭合回路，abcd的匝数为n、总电阻为r，ab中点、cd中点的连线OO/恰好位于匀强磁场的左边界线上，磁场的磁感应强度大小为B。从图示位置开始计时，线圈绕垂直于磁场的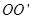
轴以角速度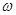
匀速转动，则下列说法中正确的是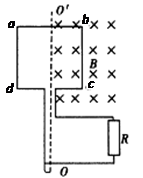
A．回路中感应电动势的瞬时表达式e = nBωL2 sinωt
B．在t =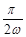 
时刻，穿过线圈的磁通量为零，磁通量变化率最大
C．从t ="0" 到t = 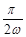时刻，电阻R产生的焦耳热为Q =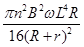 
D．从t ="0" 到t = 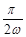时刻，通过R的电荷量q =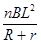 
关于速度、加速度以及匀速直线运动的有关说法中正确的是（）
| A．物体运动的速度越大，它的加速度一定越大 |
| B．物体运动的速度改变量越大，它的加速度一定越大 |
| C．位移的方向和速度的方向始终相同的运动一定是匀速直线运动 |
| D．瞬时速度和平均速度始终相同的运动一定是匀速直线运动 |
下列说法正确的是（）
| A．只有运动很慢的物体才可以看成质点 |
| B．研究一个做匀速直线运动的物体的速度时，可以不选参考系 |
| C．（n-1）s末就是指第ns初 |
| D．若物体做单向直线运动，位移就是路程 |
在下图右图中，甲、乙两图分别为测灯泡电阻R的电路图，下述说法不正确的是(）
| A．甲图的接法叫电流表外接法，乙图的接法叫电流表的内接法 |
| B．甲图中电阻测量值大于真实值，乙图中电阻测量值小于真实值 |
| C．甲图中误差由电压表分流引起，为了减小误差，应使R<<RV |
D．乙图中灯泡电阻的精确值应为 |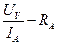
在研究微型电动机的性能时，应用如图所示的实验电路。当调节滑动变阻器R并控制电动机停止转动时，电流表和电压表的示数分别为0.50A和2.0V。重新调节R并使电动机恢复正常运转，此时电流表和电压表的示数分别为2.0A和24.0V。则这台电动机正常运转时输出功率为（）
| A．32W | B．44W | C．47W | D．48W |
在如图所示的电路中，R1、R2、R3和R4皆为定值阻，R5为可变电阻，电源的电动势为ε，内阻为r。设电流表A的读数为I，电压表V的读数为U。当R5的滑动触点向图中a端移动时（）
A I变大，U变小 B I变大，U变大
C I变小，U变大 D I变小，U变小