一宇航员为了估测某一星球表面的重力加速度和该星球的质量，在该星球的表面做自由落体实验：让小球在离地面h高处自由下落，他测出经时间t小球落地，又已知该星球的半径为R，忽略一切阻力。求：
（1）该星球表面的重力加速度g；
（2）该星球的质量M；
（3）该星球的第一宇宙速度V.
如图所示，用长为L的细线拴一个质量为m的小球，使小球在水平面内做匀速圆周运动，细线与竖直方向间的夹角为θ，求：
（1）细线的拉力F；（2） 小球圆周运动的周期T
小船在静水中的航速是4m/s，要它横渡20m宽的河流，河水流速为2m/s。
⑴ 若小船渡河时间最短，求小船过河的合速度大小和船在横渡过程中被水流推向下游的距离.
⑵ 若要小船直接到达正对岸，求船头朝向与河岸的夹角.
将一小球以3m/s的速度水平抛出，它落地时的速度大小为5m/s，求小球在空中运动的时间及位移大小. （取g＝10 m/s2）
实验室考查氢原子跃迁时的微观效应。已知氢原子能级图如图所示，氢原子质量为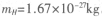
。设原来处于静止状态的大量激发态氢原子处于n=5的能级状态。
①求氢原子由高能级向低能级跃迁时，可能发射出多少种不同频率的光；
②若跃迁后光子沿某一方向飞出，且光子的动量可以用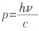
表示a为普朗克常量，v为光子频率,c为真空中光速），求发生电子跃迁后氢原子的最大反冲速率。（保留三位有效数字）
如图所示是一列简谐横波上A、B两质点的振动图象，该波由A传向B两质点沿波的传播方向上的距离
，波长大于3.0 m,求这列波的波速