已知正方形ABCD的边长为2，
，
将正方形ABCD沿对角线BD折起，使
，得到三棱锥
，如图所示。
（1）当a=2时，求证：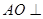
平面BCD；
（2）当二面角
的大小为
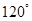时，
求二面角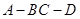
的正切值。
在平面直角坐标系
中，已知直线
与椭圆
的一条准线的交点位于
轴上，求实数
的值.
已知矩阵
的一个特征值为
，求
.
如图，圆
是
的外接圆，点
是劣弧
的中点，连结
并延长，与以
为切点的切线交于点
，求证：
.
已知函数
，
，
．
（1）若
，求证：
（ⅰ）
在
的单调减区间上也单调递减；
（ⅱ）
在
上恰有两个零点；
（2）若
，记的两个零点为
，求证：
．
如图，在平面直角坐标系
中， 已知圆
，椭圆
， 
为椭圆右顶点．过原点
且异于坐标轴的直线与椭圆
交于
两点，直线
与圆的另一交点为
，直线
与圆的另一交点为
，其中
．设直线
的斜率分别为
．
（1）求
的值；
（2）记直线
的斜率分别为
，是否存在常数
，使得
？若存在，求值；若不存在，说明理由；
（3）求证：直线
必过点．