某种书每册的成本费y(元)与印刷册数x(千册)有关,经统计得到数据如下:检验每册书的成本费y与印刷册数的倒数 之间是否具有线性相关关系,如有,求出y对x的回归方程.
之间是否具有线性相关关系,如有,求出y对x的回归方程.
| x |
1 |
2 |
3 |
5 |
10 |
20 |
30 |
50 |
100 |
200 |
| y |
10.15 |
5.52 |
4.08 |
2.85 |
2.11 |
1.62 |
1.41 |
1.30 |
1.21 |
1.15 |
设 ,
, 分别为椭圆
分别为椭圆
 的左、右焦点,过
的左、右焦点,过 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,直线
两点,直线 的倾斜角为
的倾斜角为 ,
, 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的焦距;
的焦距;
(2)如果 ,求椭圆
,求椭圆 的方程.
的方程.
已知等差数列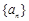 的前
的前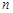 项和为
项和为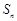 ,
,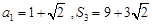
(1)求数列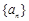 的通项公式
的通项公式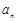 与前
与前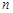 项和
项和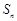 ;
;
(2)设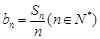 求证:数列
求证:数列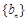 中任意不同的三项都不可能成为等比数列
中任意不同的三项都不可能成为等比数列
如图,四棱锥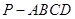 中,底面
中,底面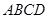 是
是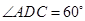 的菱形,
的菱形,
侧面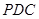 是边长为2的正三角形,且与底面
是边长为2的正三角形,且与底面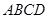 垂直,
垂直,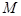 为
为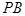 的中点.
的中点.
(1)求证: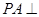 平面
平面 ;
;
(2)求二面角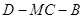 的余弦值.
的余弦值.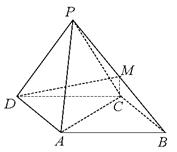
某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为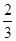 .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
(1) 随机选取1件产品,求能够通过检测的概率;
(2)随机选取3件产品,其中一等品的件数记为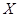 ,求
,求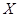 的数学期望;
的数学期望;
(3)随机选取3件产品,求这三件产品都不能通过检测的概率.
已知函数f(x)= sin2x+sinxcosx-
sin2x+sinxcosx- (xÎR).
(xÎR).
(1)若 ,求f(x)的最大值;
,求f(x)的最大值;
(2)在△ABC中,若A<B,f(A)=f(B)= ,求
,求  的值.
的值.