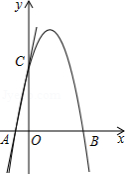
已知如图，矩形OABC的长OA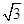，宽OC1，将△AOC沿AC翻-优题课

已知如图，矩形OABC的长OA=，宽OC=1，将△AOC沿AC翻折得△AFC.
求过A、F、C三点的抛物线解析式；
设（1）中的抛物线与矩形OABC边CB相交于点D，与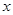轴相交于另外一点E，若点M是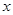轴上的点，N是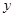轴上的点，若以点E、M、D、N为顶点的四边形是平行四边形，试求点M、N的坐标
若动点P以每秒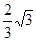个单位长度的速度从C点出发沿CB 向终点B运动，同时动点Q从A点出发以每秒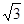个单位长度的速度沿射线AO运动，当P运动到B点时，P，Q同时停止运动.当点P运动时间t(秒)为何值时，以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似？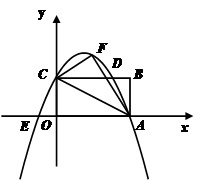

科目数学题型解答题难度中等

知识点：二次函数在给定区间上的最值

据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过 $15 m / s$ ，在一条笔直公路 $BD$ 的上方 $A$ 处有一探测仪，如平面几何图， $AD = 24 m$ ， $∠ D = 90 °$ ，第一次探测到一辆轿车从 $B$ 点匀速向 $D$ 点行驶，测得 $∠ ABD = 31 °$ ，2秒后到达 $C$ 点，测得 $∠ ACD = 50 ° (\tan 31 ° \approx 0.6$ ， $\tan 50 ° \approx 1.2$ ，结果精确到 $1 m)$

（1）求 $B$ ， $C$ 的距离．

（2）通过计算，判断此轿车是否超速．

在 $ΔABC$ 中， $BC = a$ ， $AC = b$ ， $AB = c$ ，若 $∠ C = 90 °$ ，如图1，则有 $a^{2} + b^{2} = c^{2}$ ；若 $ΔABC$ 为锐角三角形时，小明猜想： $a^{2} + b^{2} > c^{2}$ ，理由如下：如图2，过点 $A$ 作 $AD ⊥ CB$ 于点 $D$ ，设 $CD = x$ ．在 $Rt Δ ADC$ 中， $A D^{2} = b^{2} - x^{2}$ ，在 $Rt Δ ADB$ 中， $A D^{2} = c^{2} - {(a - x)}^{2}$

$∴ a^{2} + b^{2} = c^{2} + 2 ax$

$∵ a > 0$ ， $x > 0$

$∴ 2 ax > 0$

$∴ a^{2} + b^{2} > c^{2}$

$∴$ 当 $ΔABC$ 为锐角三角形时， $a^{2} + b^{2} > c^{2}$

所以小明的猜想是正确的．

（1）请你猜想，当 $ΔABC$ 为钝角三角形时， $a^{2} + b^{2}$ 与 $c^{2}$ 的大小关系．

（2）温馨提示：在图3中，作 $BC$ 边上的高．

（3）证明你猜想的结论是否正确．

甲队修路500米与乙队修路800米所用天数相同，乙队比甲队每天多修30米，问甲队每天修路多少米？

解：设甲队每天修路 $x$ 米，用含 $x$ 的代数式完成表格：

甲队每天修路长度（单位：米）	乙队每天修路长度（单位：米）	甲队修500米所用天数（单位：天）	乙队修800米所用天数（单位：天）
$x$		$\frac{500}{x}$

关系式：甲队修500米所用天数 $=$ 乙队修800米所用天数

根据关系式列方程为：　　

解得：　　

检验：　　

答：　　．

为确保信息安全，在传输时往往需加密，发送方发出一组密码 $a$ ， $b$ ， $c$ 时，则接收方对应收到的密码为 $A$ ， $B$ ， $C$ ．双方约定： $A = 2 a - b$ ， $B = 2 b$ ， $C = b + c$ ，例如发出1，2，3，则收到0，4，5

（1）当发送方发出一组密码为2，3，5时，则接收方收到的密码是多少？

（2）当接收方收到一组密码2，8，11时，则发送方发出的密码是多少？

如图，直线 $y = 5 x + 5$ 交 $x$ 轴于点 $A$ ，交 $y$ 轴于点 $C$ ，过 $A$ ， $C$ 两点的二次函数 $y = a x^{2} + 4 x + c$ 的图象交 $x$ 轴于另一点 $B$ ．

（1）求二次函数的表达式；

（2）连接 $BC$ ，点 $N$ 是线段 $BC$ 上的动点，作 $ND ⊥ x$ 轴交二次函数的图象于点 $D$ ，求线段 $ND$ 长度的最大值；

（3）若点 $H$ 为二次函数 $y = a x^{2} + 4 x + c$ 图象的顶点，点 $M (4, m)$ 是该二次函数图象上一点，在 $x$ 轴、 $y$ 轴上分别找点 $F$ ， $E$ ，使四边形 $HEFM$ 的周长最小，求出点 $F$ ， $E$ 的坐标．

温馨提示：在直角坐标系中，若点 $P$ ， $Q$ 的坐标分别为 $P (x_{1}$ ， $y_{1})$ ， $Q (x_{2}$ ， $y_{2})$ ，

当 $PQ$ 平行 $x$ 轴时，线段 $PQ$ 的长度可由公式 $PQ = | x_{1} - x_{2} |$ 求出；

当 $PQ$ 平行 $y$ 轴时，线段 $PQ$ 的长度可由公式 $PQ = | y_{1} - y_{2} |$ 求出．