如图所示，水平传送带AB的右端与在竖直面内的用内径光滑的钢管弯成的“9”形固定轨道相接，钢管内径很小.传送带的运行速度v0=4.0m/s，将质量m=1kg的可看做质点的滑块无初速地放在传送带的A端.已知传送带长度L= 4.0 m，离地高度h=0.4 m，“9”字全髙H= 0.6 m，“9”字上半部分圆弧半径R="0.1" m，滑块与传送带间的动摩擦因数μ=0.2，重力加速度g=10 m/s2，试求：
(1)滑块从传送带A端运动到B端所需要的时间；
(2)滑块滑到轨道最高点C时对轨道作用力；
(3)滑块从D点抛出后的水平射程。
如图所示，半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上，轨道之间有一条水平轨道CD相通，一小球以一定的速度先滑上甲轨道，通过动摩擦因数为μ的CD段，又滑上乙轨道，最后离开两圆轨道，若小球在两圆轨道的最高点对轨道的压力都恰好为零，试求CD段的长度.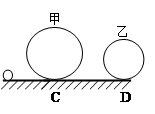
2011年8月10日，改装后的瓦良格号航空母舰进行出海航行试验，中国成为拥有航空母舰的国家之一。已知该航空母舰飞行甲板长度为L="300" m,某种战斗机在航空母舰上起飞过程中的最大加速度为a="4.5" m/s2，飞机速度要达到v="60" m/s才能安全起飞。
1）.如果航空母舰静止，战斗机被弹射装置弹出后开始加速,要保证飞机起飞安全，战斗机被弹射装置弹出时的速度至少是多大？
2）.如果航空母舰匀速前进，在没有弹射装置的情况下，要保证飞机安全起飞，航空母舰前进的速度至少是多大？
如图所示，一带电量为
、质量为
的小球，从距地面高
处以一定的初速度水平抛出，在距抛出点水平距离为
处有根管口比小球略大的竖直细管，管的上口距地面
。为了使小球能无碰撞地通过管子，可在管子上方整个区域内加一水平向左的匀强电场，求：
（1）小球的初速度
的大小；
（2）应加电场的场强大小；
（3）小球落地时的动能。
如图所示，变阻器的滑片p位于其中点，变阻器的总电阻为2kΩ。
（1）当在ab两点间加上120V电压时，接在cd间的电压表读数为40V，试求此时变阻器消耗的总功率；
（2）当在cd两点间加上40V电压时，接在ab间的上述电压表读数为多少？
密立根油滴实验进一步证实了电子的存在，揭示了电荷的非连续性.如图所示是密立根实验的原理示意图，设小油滴质量为m，调节两板间电势差为U,当小油滴悬浮不动时，测出两板间距离为d，则（1）分析判断哪个极板带正电？（2）小油滴的电荷量q是多少？