有a、b、c、d四颗地球卫星,a还未发射,在地球赤道上随地球表面一起转动,b处于地面附近的近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星,各卫星排列位置如图,则有 ( )
| A.a的向心加速度等于重力加速度g |
| B.b在相同时间内转过的弧长最长 |
| C.c在4小时内转过的圆心角是π/6 |
| D.d的运动周期有可能是20小时 |
)[选项3-3]下列说法正确的是()
| A.物体从外界吸收热量,其内能一定增加 |
| B.物体对外界做功,其内能一定减少 |
| C.气体温度升高时,每个分子运动速率都会增大 |
| D.电冰箱的工作过程表明,热量可以从低温物体向高温物体传递 |
如图所示电路中,电源电动势E恒定,内阻 ,两电表均为理想电表,定值电阻
,两电表均为理想电表,定值电阻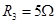 .当开关K断开与闭合时,ab段电路消耗的电功率相等.则下列说法正确的是( )
.当开关K断开与闭合时,ab段电路消耗的电功率相等.则下列说法正确的是( )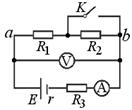
A.电阻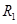 、 、 可能分别为3Ω、6Ω 可能分别为3Ω、6Ω |
B.电阻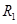 、 、 可能分别为4Ω、5Ω 可能分别为4Ω、5Ω |
| C.开关K断开时电压表的示数一定小于K闭合时的示数 |
D.开关K断开与闭合时,电压表的示数变化量大小与电流表的示数变化量大小之比一定等于 |
闭合矩形导线框abcd固定在匀强磁场中,磁场的方向与导线框所在平面垂直,磁感应强度B随时间t变化的的规律如图所示.规定垂直纸面向里为磁场的正方向,abcda的方向为线框中感应电流的正方向,水平向右为安培力的正方向.关于线框中的电流i与ad边所受的安培力F随时间t变化的图象,下列选项正确的是( )
2013年12月14日21时11分,嫦娥三号成功实现月面软着陆,中国成为世界上第三个在月球上实现软着陆的国家.如图所示,嫦娥三号经历漫长的地月旅行后,首次在距月表100km的环月轨道上绕月球做圆周运动.运动到A点时变推力发动机开机工作,嫦娥三号开始快速变轨,变轨后在近月点B距月球表面15km的椭圆轨道上绕月运行;当运动到B点时,变推力发动机再次开机,嫦娥三号从距月面15km处实施动力下降.关于嫦娥三号探月之旅,下列说法正确的是( )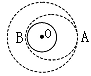
| A.在A点变轨时,嫦娥三号的机械能增加 |
| B.在A点变轨时,发动机的推力和嫦娥三号运动方向相反 |
| C.在A点变轨后,嫦娥三号在椭圆轨道上运行的周期比圆轨道周期长 |
| D.在A点变轨后沿椭圆轨道向B点运动的过程中,嫦娥三号的加速度逐渐减小 |
如图所示,实线为一匀强电场的电场线,两个带电粒子甲和乙分别从A、C两点以垂直于电场线方向的相同大小的初速度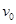 同时射入电场,粒子在电场中仅受电场力作用,其运动轨迹分别为图中虚线ABC与CDA所示.若甲是带正电的粒子,则下列说法正确的是
同时射入电场,粒子在电场中仅受电场力作用,其运动轨迹分别为图中虚线ABC与CDA所示.若甲是带正电的粒子,则下列说法正确的是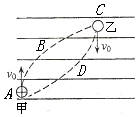
A.乙也是带正电的粒子 B.A点的电势低于C点的电势
C.甲乙两粒子的电势能均减小 D.甲乙两粒子的电量一定相等