某公司组织部分员工到一博览会的A、B、C、D、E五个展馆参观,公司所购门票种类、数量绘制成的条形和扇形统计图如图所示.


请根据统计图回答下列问题:
B馆门票多少张?C馆门票占所购门票的比例是多少?
若
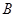 馆门票仅剩下一张,而员工小明和小华都想要,他们决定采用抽扑克牌的
馆门票仅剩下一张,而员工小明和小华都想要,他们决定采用抽扑克牌的
方法来确定,规则是:“将同一副牌中正面分别标有数字1,2,3,4的四张牌洗匀
后,背面朝上放置在桌面上,每人随机抽一次且一次只抽一张;一人抽后记下数字,
将牌放回洗匀背面朝上放置在桌面上,再由另一人抽.若抽出的两次数字之积为偶
数则小明获得门票,反之小华获得门票.” 请用画树状图或列表的方法计算出小明和
小华获得门票的概率,并说明这个规则对双方是否公平.
已知线段 ,
,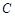 为
为 的中点,
的中点, 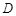 为
为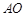 上一点,连接
上一点,连接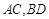 交于
交于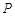 点.
点.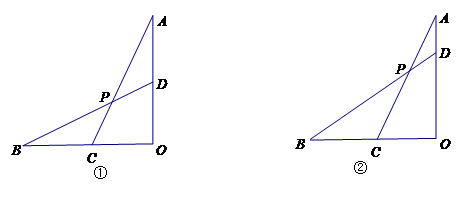
(1)如图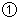 ,当OA=OB且
,当OA=OB且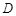 为
为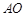 中点时,求
中点时,求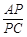 的值;
的值;
(2)如图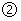 ,当OA=OB,
,当OA=OB,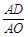 =
=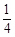 时,求tan∠
时,求tan∠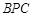 .
.
某商店原来将进货价为8元的商品按10元售出,每天可销售200件.现在采用提高售价,减少进货量的方法来增加利润,已知每件商品涨价1元,每天的销售量就减少20件.设这种商品每个涨价 元.
元.
(1)填空:
原来每件商品的利润是 元,
涨价后每件商品的实际利润是 元(可用含 的代数式表示);
的代数式表示);
(2)为了使每天获得700元的利润,售价应定为多少
已知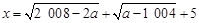 ,其中
,其中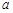 是实数,将式子
是实数,将式子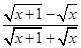 +
+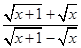 化简并求值.
化简并求值.
如果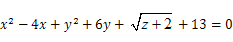 ,求
,求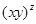 的值.
的值.
阅读理解:一个分数,如果分子加上9,结果是 ;如果分子加上4,结果是
;如果分子加上4,结果是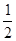 .求原来这个分数.
.求原来这个分数.
解:设这个分数为 ,则,
,则,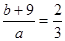 ,
, .
. .
.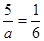 .
. .
.
所以原来这个分数是 .
.
请你根据对上面计算方法的理解,解答下题:
一个分数,如果分子加上2,结果是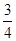 ;如果分子减去3,结果是
;如果分子减去3,结果是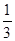 .
.
求原来这个分数.