空间有一竖直向下的匀强磁场，磁感应强度B＝0.8T，两相同的长方形金属板MN、PQ竖直平行放置，俯视如图。两板间距L＝0.20m，与两板间距等长的金属棒AB垂直放在金属板上，可无摩擦滑动，其电阻R0＝4Ω，金属板的右边接有如图电路，电阻R1＝4Ω，R,2＝2Ω。现有不计重力的带电粒子以v0=2m/s的水平初速度射入两板间，问：
（1）欲使粒子能保持水平方向做匀速直线运动，金属棒AB运动速度的大小和方向；
（2）若金属棒AB保持以（1）中速度做匀速滑动，作用在AB上的外力多大；
（3）若使金属棒在稳定运动过程中突然停止，则在停止运动的瞬间，作用在棒上的磁场力大小与方向。
边长为L＝0.2 m的正方形区域内有垂直纸面向里的匀强磁场，穿过该区域磁场的磁感应强度随时间变化的图象如图乙所示。将边长为L/2，匝数n＝100，线圈电阻r＝1.0 Ω的正方形线圈abcd放入磁场，线圈所在平面与磁感线垂直，如图甲所示。求：
(1)回路中感应电流的方向及磁感应强度的变化率
；
(2)在0～4.0 s内通过线圈的电荷量q；
(3)0～6.0 s内整个闭合电路中产生的热量。
如图所示，在半径为
的圆形区域内有垂直纸面向里的匀强磁场，磁感应强度为B，圆形区域右侧有一竖直感光板，圆弧顶点P有一速率为v0的带正电的粒子平行于纸面进入磁场，已知粒子的质量为m，电荷量为q，粒子重力不计．
(1)若粒子对准圆心射入，求它在磁场中运动的时间；
(2)若粒子对准圆心射入，且速率为
，求它打到感光板上时速度的垂直分量；
(3)若粒子以速率v0从P点以任意角射入，试证明它离开磁场后均垂直打在感光板上．
回旋加速器是用于加速带电粒子流，使之获得很大动能的仪器，其核心部分是两个D形金属扁盒，两盒分别和一高频交流电源两极相接，以便在盒间狭缝中形成匀强电场，使粒子每穿过狭缝都得到加速；两盒放在匀强磁场中，磁场方向垂直于盒底面．离子源置于盒的圆心，释放出电量为q、质量为m的离子，离子最大回旋半径为Rm，磁场强度为B，其运动轨迹如图所示．求：
(1)离子离开加速器时速度多大？
(2)设离子初速度为零，两D形盒间电场的电势差为U，盒间距离为d，求加速到上述能量所需时间（粒子在缝中时间不忽略）。
质量均为m的两个可视为质点的小球A、B，分别被长为L的绝缘细线悬挂在同一点O，给A、B分别带上一定量的正电荷，并用水平向右的外力作用在A球上，平衡以后，悬挂A球的细线竖直，悬挂B球的细线向右偏60°角，如图所示．若A球的带电量为q，则：
（1）B球的带量为多少；
（2）水平外力多大．
如图所示，在平行金属带电极板MN电场中将电荷量为﹣4×10﹣6C的点电荷从A点移到M板，电场力做负功8×10﹣4J，把该点电荷从A点移到N板，电场力做正功为4×10﹣4，N板接地．则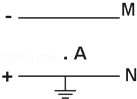
（1）A点的电势φA是多少？
（2）UMN等于多少伏？
（3）M板的电势φM是多少？