(18分)如图甲,电阻不计的轨道MON与PRQ平行放置，ON及RQ与水平面的倾角
=53°，MO及PR部分的匀强磁场竖直向下，ON及RQ部分的磁场平行轨道向下，磁场的磁感应强度大小相同，两根相同的导体棒ab和cd分别放置在导轨上，与导轨垂直并始终接触良好。棒的质量m=1.0kg，R=1.0
，长度与导轨间距相同，L=1.0m，棒与导轨间动摩擦因数
=0.5，现对ab棒施加一个方向向右，大力随乙图规律变化的力F的作用，同时由静止释放cd棒，则ab棒做初速度为零的匀加速直线运动，g取10m/s2，求：
(1)ab棒的加速度大小；
(2)磁感应强度B的大小；
(3)若已知在前2s内外力做功W=30J，求这一过程中电路产生的焦耳热；
(3)求cd棒达到最大速度所需的时间.
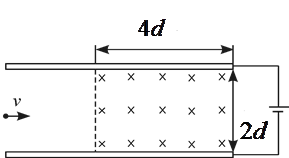
如图所示，两块水平放置、相距为
的长金属板接在电压可调的电源上。两板之间的右侧长度为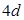
的区域存在方向垂直纸面向里的匀强磁场，磁感应强度为
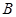。喷墨打印机的喷口可在两极板左侧上下自由移动，并且从喷口连续不断喷出质量均为
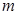、速度水平且大小相等、带等量电荷的墨滴。调节电源电压至
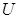，使墨滴在电场的左侧区域恰能沿水平方向向右做匀速直线运动。（重力加速度为
）
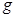（1）判断墨滴所带电荷的种类，并求其电荷量；
（2）要使墨滴不从两板间射出，求墨滴的入射速率应满足的条件。
一小型发电站通过升压、降压变压器把电能输给用户。已知发电机的输出功率是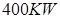
，端电压为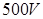
，升压变压器原、副线圈的匝数比为1:8，两变压器间输电线的总电阻为
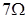，降压变压器的输出电压为
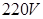，不计变压器的损耗。求：
（1）升压变压器的副线圈两端电压；
（2）输电导线上的功率损失；
（3）降压变压器原、副线圈的匝数比；
（4）用户得到的功率。
如图所示，水平面上有两根相距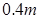
的足够长的光滑平行金属导轨
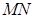和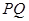
，它们的电阻可忽略不计，在
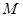和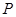
之间接有阻值为
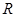的定值电阻。导体棒
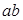长
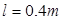，其电阻为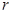
，与导轨接触良好。整个装置处于方向竖直向上的匀强磁场中，磁感应强度
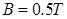。现在在导体棒ab上施加一个水平向右的力
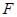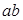，使以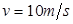
的速度向右做匀速运动时，求：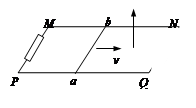
⑴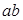中的感应电动势多大？
⑵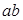中电流的方向如何？
⑶若定值电阻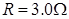
，导体棒的电阻
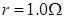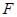，则多大？
某理想变压器的原、副线圈匝数比n1：n2=55:9，原线圈上的正弦交变电压U1=220V，试求：（1）副线圈上的输出电压为多大？
（2）若副线圈输出的功率为10W变压器的输入功率为多少？
计算下列物体的加速度：
(1)汽车启动时，从静止开始做匀加速直线运动，经10s速度达到72km/h；
(2)沿光滑水平地面以12m/s运动的小球,撞墙后以原来速度大小反弹回来,与墙壁接触时间为0.2s。