2009年某市出口贸易总值为22.52亿美元，至2011年出口贸易总值达到50.67亿美元，反映了两年来该市出口贸易的高速增长．
（1）求这两年该市出口贸易的年平均增长率；
（2）按这样的速度增长，请你预测2012年该市的出口贸易总值．
（提示：2252=4×563，5067=9×563）
如图所示，在△ABC中，AC＝10，BC＝17，CD＝8，AD＝6．
求：（1）BD的长；
（2）△ABC的面积．
如图，AB=AE，∠1=∠2，∠C=∠D．求证：△ABC≌△AED．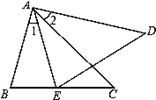
（1）计算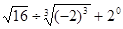
（2）解方程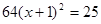
在平面直角坐标系
中，对于任意三点
、
、
的“矩面积”，给出如下定义：“水平底”
：任意两点横坐标差的最大值，“铅垂高”
：任意两点纵坐标差的最大值，则“矩面积”
．
例如：三点坐标分别为
，
，
，则“水平底”
，“铅垂高”
，“矩面积”
．
（1）已知点
，，
．
①若、、
三点的“矩面积”为
，求点的坐标；
②、、三点的“矩面积”的最小值为
（2）已知点
，
，
，其中
．若
、
、
三点的“矩面积”的为8，求
的取值范围；
如图，在直角坐标系中，Rt△OAB的直角顶点A在x轴上，OA=4，AB=3．动
点M从点A出发，以每秒1个单位长度的速度，沿AO向终点O移动；同时点N从点O出发，以每秒1．25个单位长度的速度，沿OB向终点B移动．当两个动点运动了x秒（0＜x＜4）时，解答下列问题：
（1）求点N的坐标（用含x的代数式表示）；
（2）设△OMN的面积是S，求S与x之间的函数表达式；当x为何值时，S有最大值？最大值是多少？
（3）在两个动点运动过程中，是否存在某一时刻，使△OMN是直角三角形？若存在，求出x的值；若不存在，请说明理由．