若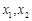 是关于
是关于 的一元二次方程
的一元二次方程 的两个根,则方程的两个根
的两个根,则方程的两个根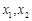 和系数
和系数 有如下关系:
有如下关系: . 我们把它们称为根与系数关系定理. 如果设二次函数
. 我们把它们称为根与系数关系定理. 如果设二次函数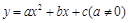 的图象与x轴的两个交点为
的图象与x轴的两个交点为 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
请你参考以上定理和结论,解答下列问题:
设二次函数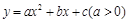 的图象与x轴的两个交点为
的图象与x轴的两个交点为 ,抛物线的顶点为
,抛物线的顶点为 ,显然
,显然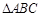 为等腰三角形.
为等腰三角形.
(1)当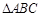 为等腰直角三角形时,求
为等腰直角三角形时,求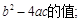
(2)当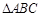 为等边三角形时,求
为等边三角形时,求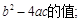
关于x的一元二次方程x2-(m-1)x+2m-1=0:
(1)若其根的判别式为-20,求m的值;
(2)设该方程的两个实数根为x1 ,x2 ,且x12+x22=10,求m的值.
如图,在△ABC中,∠B=45°,∠C=60°,AB=3 ,AD⊥BC于D,求DC.
,AD⊥BC于D,求DC.
(1)解方程:
(2)计算:
如图,对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).
(1)求点B的坐标;
(2)已知a=1,C为抛物线与y轴的交点.
①若点P在抛物线上,且S△POC=4S△BOC.求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
某体育休闲超市购进一种成本为20元/个的风筝,据市场调查分析,若按25元/个销售,一个月能售出70个,在此基础上,售价每涨1元/个,月销售量就减少2个.设这种风筝的销售单价为x(元/个),该超市每月销售这种风筝的所获得的利润为y(元),针对这种风筝的销售情况,请解答下列问题:
(1)用含x的代数式分别表示出每个风筝的销售利润为 元,每月卖出的风筝的个数是 个;
(2)求y与x之间的函数关系式;
(3)若该超市想在每月销售这种风筝的成本不超过800元的情况下,使得月销售利润达到600元,则每个风筝的售价应定为多少元?