问题背景:在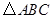 中,
中,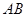 、
、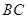 、
、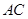 三边的长分别为
三边的长分别为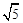 、
、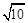 、
、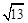 ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点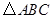 (即
(即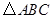 三个顶点都在小正方形的顶点处),如图①所示.这样不需求
三个顶点都在小正方形的顶点处),如图①所示.这样不需求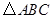 的高,而借用网格就能计算出它的面积.
的高,而借用网格就能计算出它的面积.请你将
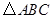 的面积直接填写在横线上._________________________思维拓展:
的面积直接填写在横线上._________________________思维拓展:我们把上述求
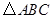 面积的方法叫做构图法.若
面积的方法叫做构图法.若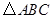 三边的长分别为
三边的长分别为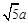 、
、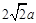 、
、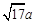 (
(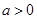 ),请利用图②的正方形网格(每个小正方形的边长为
),请利用图②的正方形网格(每个小正方形的边长为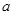 )画出相应的
)画出相应的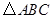 ,并求出它的面积.探索创新:
,并求出它的面积.探索创新:若
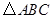 三边的长分别为
三边的长分别为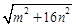 、
、 、
、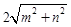 (
(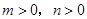 ,且
,且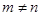 ),试运用构图法求出这三角形的面积.
),试运用构图法求出这三角形的面积.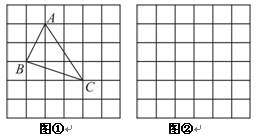
一家化工厂原来每月利润为120万元,从今年1月起安装使用回收净化设备(安装时间不计),一方面改善了环境,另一方面大大降低原料成本.据测算,使用回收净化设备后的1至x月(1≤x≤12)的利润的月平均值w(万元)满足w=10x+90,第二年的月利润稳定在第1年的第12个月的水平.
(1)设使用回收净化设备后的1至x月(1≤x≤12)的利润和为y,写出y关于x的函数关系式,并求前几个月的利润和等于700万元;
(2)当x为何值时,使用回收净化设备后的1至x月的利润和与不安装回收净化设备时x个月的利润和相等;
(3)求使用回收净化设备后两年的利润总和.
在一个边长为a(单位:cm)的正方形ABCD中.
(1)如图1,如果N是AD中点,F为AB中点,连接DF,CN.
①求证:DF=CN;
②连接AC.求DH:HE: EF的值;
(2)如图2,如果点E、M分别是线段AC、CD上的动点,假设点E从点A出发,以 cm/s速度沿AC向点C运动,同时点M从点C出发,以1cm/s的速度沿CD向点D运动,运动时间为t(t>0),连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.判断命题“当点F是边AB中点时,则点M是边CD的三等分点”的真假,并说明理由.
cm/s速度沿AC向点C运动,同时点M从点C出发,以1cm/s的速度沿CD向点D运动,运动时间为t(t>0),连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.判断命题“当点F是边AB中点时,则点M是边CD的三等分点”的真假,并说明理由.
如图,已知直线y=-x+4与反比例函数y=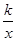 的图象相交于点A(-2,a),并且与x轴相交于点B。
的图象相交于点A(-2,a),并且与x轴相交于点B。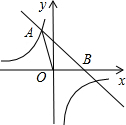
(1)求a的值;
(2)求反比例函数的表达式;
(3)求△AOB的面积。
某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点.再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°.已知山顶C点处的高度是600米.
(1)求斜坡B点处的高度;
(2)求斜坡AB的坡度.
某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小
球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每
消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返
还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.