1920年，英国物理学家卢瑟福曾预言：可能有一种质量与质子相近的不带电的中性粒子存在，他把它叫做中子。1930年发现，在真空条件下用a射线轰击铍(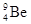
)时，会产生一种看不见的、贯穿能力极强的不知名射线和另一种新粒子。经过研究发现，这种不知名射线具有如下的特点：① 在任意方向的磁场中均不发生偏转；② 这种射线的速度不到光速的十分之一；③ 用它轰击含有静止的氢核的物质，可以把氢核打出来。用它轰击含有静止的氮核的物质，可以把氮核打出来。并且被打出的氢核的最大速度vH和被打出的氮核的最大速度vN之比等于15 : 2。若该射线中的粒子均具有相同的能量，与氢核和氮核均发生正碰，且碰撞中没有机械能的损失。已知氢核的质量MH与氮核的质量MN之比等于1 : 14。
（1）写出a射线轰击铍核的核反应方程。
（2）试根据上面所述的各种情况，通过具体计算说明该射线是由中子组成，而不是g射线。
如图所示，在水平地面上固定一倾角θ=37°、表面光滑的斜面，物体A以
的初速度沿斜面上滑，同时在物体A的正上方，物体B以某一初速度
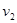水平抛出。如果当A上滑到最高点时恰好被B物体击中（A、B均可看作质点， sin37°=0.6，cos37°=0.8，g取10m/s2）。求：
（1）物体A上滑到最高点所用的时间t；
（2）物体B抛出时的初速度。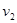
（3）物体A、B间初始位置的高度差h。
如图，传送带与地面倾角θ=30°，AB长度为
，传送带以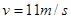
的速率逆时针转动.在传送带上端A无初速度地放上一个质量为
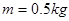的物体，它与传送带之间的动摩擦因数为
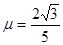,取
，则：
（1）从物体开始运动至物体刚与传送带达到共同速度这一过程中,传送带的摩擦力对物体做了多少功?
（2）物体从与传送带达到共同速度的瞬间至滑到B端的过程中，传送带的摩擦力对物体又做了多少功?
如图所示，轻杆长为3L， 在杆的A、B两端分别固定质量均为
的球A和球B，杆上距球A为L处的点O装在光滑水平转动轴上，杆和球在竖直面内转动，已知球A运动到最高点时，球A对杆恰好无作用力。求： 
（1）球A在最高点时的角速度大小；
（2）球A在最高点时，杆对水平轴的作用力的大小和方向。
如图所示，在距地面高为H=45m处，有一小球A以初速度
水平抛出，与此同时，在A的正下方有一物块B也以相同的初速度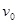
同方向滑出，B与地面间的动摩擦因数为
。A、B均可视为质点，空气阻力不计，重力加速度取
，求：
（1）A球落地时间及其抛出的水平距离。
（2）A球落地时，A、B相距多远。
在某星球上，宇航员用弹簧秤称得质量为m的砝码重力为F，乘宇宙飞船在靠近该星球表面空间飞行，测得其环绕周期为T。根据上述数据，试求该星球的质量。