正负电子对撞机的最后部分的简化示意如图(1)所示(俯视图),位于水平面内的粗实线所示的圆环形真空管道是正、负电子作圆运动的“容器”,经过加速器加速后的正、负电子被分别引入该管道时,具有相等的速率v,它们沿管道向相反的方向运动。在管道内控制它们转弯的是一系列圆形电磁铁,即图中的A1、A2、A3……An,共n个,均匀分布在整个圆周上(图中只示意性地用细实线画了几个,其余的用细虚线表示),每个电磁铁内的磁场都是匀强磁场,并且磁感应强度都相同,方向竖直向下,磁场区域都是直径为d的圆形。改变电磁铁内电流的大小,就可改变磁场的磁感应强度,从而改变电子偏转的角度。经过精确的调整,首先实现电子在环形管道中沿图中粗虚线所示的轨迹运动,这时电子经过每个电磁铁时射入点和射出点都在电磁铁的同一条直径的两端,如图(2)所示。这就为进一步实现正、负电子的对撞作好了准备。
(1)试确定正、负电子在管道内各是沿什么方向旋转的。
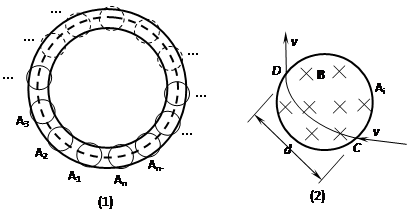 |
(2)已知正、负电子的质量都是m,所带电荷都是元电荷e,重力可不计。求电磁铁内匀强磁场的磁感应强度B的大小。
如图,两倾角为θ、间距为l的光滑金属平行轨道,轨道间接有电阻R,导轨电阻不计。轨道平面处于垂直平面向上、磁感应强度为B的匀强磁场中。有一质量为m、长为l、电阻为r的导体棒,从轨道上某处由静止开始下滑距离x时达最大速度。则从导体棒开始下滑到达到最大速度的过程中,下列说法中正确的是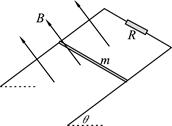
| A.导体棒做变加速直线运动 |
B.导体棒最大速度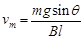 |
C.通过导体棒的电量 |
D.电路中产生的焦耳热 |
质量为2kg的平板车B上表面水平,原来静止在光滑水平面上,平板车一端静止着一块质量为2kg的物体A,一颗质量为0.01kg的子弹以600m/s的速度水平瞬间射穿A后,速度变为100m/s。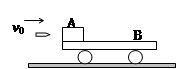
(i)若A不会滑离B,求B的最大速度;
(ii)计算A B摩擦损失的机械能。
(9分)如图,在真空中波长为600 nm的激光束从A点射入圆柱形玻璃介质。若该激光束经折射后从B点射出,射出玻璃与射入玻璃的光线夹角为30°,AB孤所对的圆心角为120°,求该激光束在玻璃中的波长。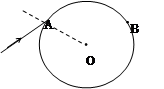
如图,由U形管和细管连接的玻璃泡A、B和C浸泡在温度均为0°C的水槽中,B的容积是A的3倍。阀门S将A和B两部分隔开。A内为真空,B和C内都充有气体。U形管内左边水银柱比右边的低60mm。打开阀门S,整个系统稳定后,U形管内左右水银柱高度相等。假设U形管和细管中的气体体积远小于玻璃泡的容积。
(i)求玻璃泡C中气体的压强(以mmHg为单位);
(ii)将右侧水槽的水从0°C加热到一定温度时,U形管内左右水银柱高度差又为60mm,求加热后右侧水槽的水温。
如图所示,在平面坐标系xoy内,第Ⅱ、Ⅲ象限内存在沿y轴正方向的匀强电场,第Ⅰ、Ⅳ象限内存在半径为L的圆形匀强磁场,磁场圆心在M(L,0)点,磁场方向垂直于坐标平面向外,一带正电粒子从第Ⅲ象限中的Q(-2L,-L)点以速度v0沿x轴正方向射出,恰好从坐标原点O进入磁场,从P(2L,0)点射出磁场。不计粒子重力。求:
(1)电场强度与磁感应强度的大小之比;
(2)粒子在磁场与电场中运动的时间之比。