如图1，点A在反比例函数y=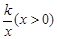
的图象上，AC⊥x轴，垂足为C，且△AOC的面积为
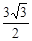.(1)求反比例函数的解析式；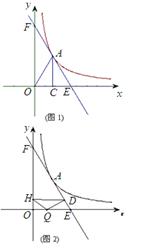
(2)当点A的横坐标为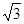
，过点A的直线交x、y轴于E、F两点，且△EOF以点A为外心，求这条直线的解析式；
(3)如图2，在(2)下，若Q是OE上不与O、E重合的任意一点，QD⊥EF于D，DH⊥y轴于H，在线段OE上是否存在点Q，使QH∥EF？若存在这样的点，请求出点Q的坐标；若不存在，请说明理由.
已知y＝y1＋y2，y1与x2成正比例，y2与x－2成正比例，当x＝1时，y＝0，当x＝－3时，y＝4．求x＝3时，y的值．
已知有两人分别骑自行车和摩托车沿着相同的路线从甲地到乙地，如图反映的是这两个人在行驶过程中时间和路程的关系，请根据图象回答下列问题：
(1)甲地与乙地相距多少千米？两人分别用了几个小时才到达乙地？谁先到达乙地？先到者早到多长时间？
(2)分别描述在这个过程中自行车和摩托车的行驶状态；
(3)求摩托车行驶的平均速度．
某商店零售一种商品，其质量x(kg)与售价y(元)之间的关系如下表：
| x／kg |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| y／元 |
2.4 |
4.8 |
7.2 |
9.6 |
12 |
14.4 |
16.8 |
19.2 |
根据销售经验可知，在此处零买这种商品的顾客所买商品均未超过8kg．
(1)由上表推出售价y(元)关于质量x(kg)的函数解析式，并画出函数的图象；
(2)李大婶购买这种商品5.5kg，应付多少元钱？
一列快车从甲地驶往乙地，一列特快车从乙地驶往甲地，快车的速度为100km／h，特快车的速度为150km／h，甲、乙两地之间的距离为1000km，两车同时出发，则能大致表示两车之间的距离y(km)与快车行驶时间t(h)之间的函数关系的图象是( )
A． |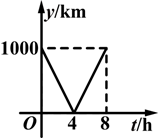
B． |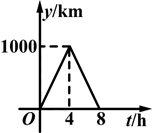
C． |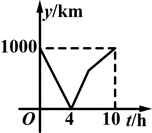
D． |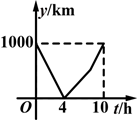
已知函数y＝2x－1．
(1)试判断点A(－1，3)和点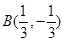
是否在此函数的图象上；
(2)已知点C(a，a＋1)在此函数的图象上，求a的值．