如图1，二次函数y=ax2+bx+c(a≠0)的图像与x轴交于点A、点B，与y轴交于点C，且A、B两点的坐标分别是(4，0)、(0，－2)，tan∠BCO＝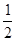
(1)求抛物线解析式；(2)点M为抛物线上一点，若以MB为直径的圆与直线BC相切于点B，求点M的坐标；(3) 如图2，若点P是抛物线上的动点，点Q是直线y=－x的动点，是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形；如果存在，请求出点P的坐标，如果不存在，请说明理由．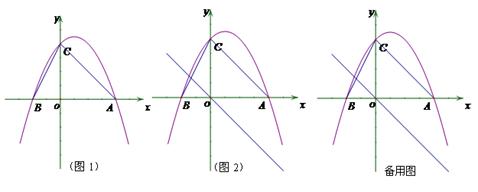
解方程：
如图，已知弦AB与半径相等，连结OB，并延长使BC=OB．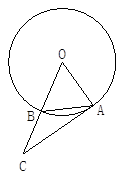
（1）问AC与⊙O有什么关系．
（2）请你在⊙O上找出一点D，使AD=AC（自己完成作图，并证明你的结论）．
如图，C是⊙O的直径AB延长线上一点，过点C作⊙O的切线CD，D为切点，连结AD，OD，BD．请根据图中给出的已知条件（不再标注字母，不再添加辅助线）写出两个你认为正确的结论．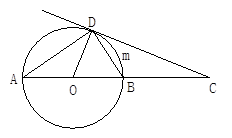
如图所示，⊙I是△ABC的内切圆，AB=9，BC=8，CA=10，点D、E分别为AB、AC上的点，且DE是⊙I的切线，求△ADE的周长．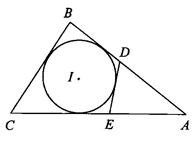
如图，已知扇形AOB的半径为12，OA⊥OB，C为OB上一点，以OA为直径的半圆O1与以BC为直径的半圆O2相切于点D．求图中阴影部分面积．