已知抛物线L:
(1)证明:不论k取何值,抛物线L的顶点C总在抛物线 上;
上;
(2)已知 时,抛物线L和x轴有两个不同的交点A、B,求A、B间距取得最大值时k的值;
时,抛物线L和x轴有两个不同的交点A、B,求A、B间距取得最大值时k的值;
(3)在(2)A、B间距取得最大值条件下(点A在点B的右侧),直线y=ax+b是经过点A,且与抛物线L相交于点D的直线. 问是否存在点D,使△ABD为等边三角形,如果存在,请写出此时直线AD的解析式;如果不存在,请说明理由.
如图,在平面直角坐标系中,已知二次函数 图象的顶点为 ,与 轴交于点 ,异于顶点 的点 在该函数图象上.
(1)当 时,求 的值.
(2)当 时,若点 在第一象限内,结合图象,求当 时,自变量 的取值范围.
(3)作直线 与 轴相交于点 .当点 在 轴上方,且在线段 上时,求 的取值范围.

如图,在 中, , , .
(1)求 边上的高线长.
(2)点 为线段 的中点,点 在边 上,连结 ,沿 将 折叠得到 .
①如图2,当点 落在 上时,求 的度数.
②如图3,连结 ,当 时,求 的长.
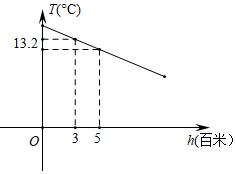
某地区山峰的高度每增加1百米,气温大约降低 ,气温 和高度 (百米)的函数关系如图所示.
请根据图象解决下列问题:
(1)求高度为5百米时的气温;
(2)求 关于 的函数表达式;
(3)测得山顶的气温为 ,求该山峰的高度.
如图, 的半径 , 于点 , .
(1)求弦 的长.
(2)求 的长.

某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如图两幅不完整的统计图表.请根据图表信息回答下列问题:
抽取的学生最喜爱体育锻炼项目的统计表
|
类别 |
项目 |
人数(人 |
|
|
跳绳 |
59 |
|
|
健身操 |
▲ |
|
|
俯卧撑 |
31 |
|
|
开合跳 |
▲ |
|
|
其它 |
22 |
(1)求参与问卷调查的学生总人数.
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.
