如图,半径为 的半球 的底面圆 在平面 内,过点 作平面 的垂线交半球面于点 ,过圆 的直径 作平面 成 角的平面与半球面相交,所得交线上到平面 的距离最大的点为 ,该交线上的一点 满足 ,则 、 两点间的球面距离为()

| A. | B. | C. | D. |
函数f(x)=ax+b-1的图像经过一,二,四象限,则有( )
| A.0<a<1,0<b<1 |
| B.0<a<1,b>1 |
| C.a>1,b>0 |
| D.a>1,b<0 |
由函数y=log2x的图像经过( )的变化,就变为y=log2(2-x)的图像
| A.先关于x轴对称,再向左平移2个单位 |
| B.先关于x轴对称,再向右平移2个单位 |
| C.先关于y轴对称,再向左平移2个单位 |
| D.先关于y轴对称,再向右平移2个单位 |
计算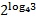 =()
=()
A. |
B.2 | C.3 | D.4 |
函数f(x)是定义在R上的偶函数,且满足f(x+2)=f(x),当x∈[0,1]时,f(x)=2x,若方程ax+a-f(x)=0(a>0)恰有三个不相等的实数根,则实数a的取值范围是()
A.(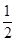 ,1) ,1) |
B.[0,2] | C.(1,2) | D.[1,+∞) |
已知点F是双曲线 (a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,△ABE是直角三角形,则该双曲线的离心率是()
(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,△ABE是直角三角形,则该双曲线的离心率是()
A、3 B、2 C、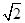 D、
D、