在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2”拓展到空间,类比平面几何的勾股定理,“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直,则可得”猜想正确的是( )
A.AB2+AC2+ AD2=BC2 +CD2 +BD2 B.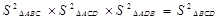
C. D.AB2×AC2×AD2=BC2×CD2×BD2
D.AB2×AC2×AD2=BC2×CD2×BD2
已知样本:12,7,11,12,11,12,10,10,9,8,13,12,10,9,6,11,8,9,8,10,那么频率为0.25的样本的范围是()
| A.[5.5,7.5) | B.[7.5,9.5) | C.[9.5,11.5) | D.[11.5,13.5) |
如右图是某电视台综艺节目举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
| A.84; 4.84 | B.84; 1.6 | C.85; 4 | D.85; 1.6 |
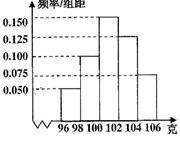
某工厂对一批产品进行了抽样检测.右图是根据
抽样检测后的产品净重数据绘制的频率分布直方
图,已知样本中产品净重小于100克的个数是36,
则样本中净重在[98,104)的产品的个数是( )
| A.90 | B.75 | C. 60 | D.45 |
某单位有职工160人,其中业务员有104人,管理人员32人,后勤服务人员24人,现用分层抽样法从中抽取一容量为20的样本,则抽取管理人员( )
| A.3人 | B.2人 | C.7人 | D.12人 |
从 个同类产品(其中
个同类产品(其中 个是正品,
个是正品, 个是次品)中任意抽取
个是次品)中任意抽取 个的必然事件是()
个的必然事件是()
A. 个都是正品 个都是正品 |
B.至少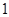 个是次品 个是次品 |
C. 个都是次品 个都是次品 |
D.至少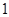 个正品 个正品 |