在梯形ABCD中，DC∥AB，DE⊥AB于点E。
阅读理解：在图一中，延长梯形ABCD的两腰AD，BC交于点P，过点D作DF∥CB交AB于点F，得到图二；四边形BCDF的面积为S，△ADF的面积为S1，△PDC的面积为S2。
解决问题：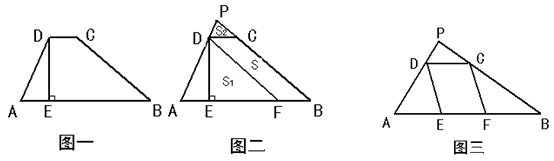
⑴在图一中，若DC=2，AB=8，DE=3，则S = ，S1 = ，S2 = ，则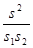
= 。
⑵在图二中，若AB=a，DC=b，DE=h，则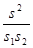= ，并写出理由。
拓展应用：如图三，现有一块地△PAB需进行美化，□DEFC的四个顶点在△PAB的三边上，且种植茉莉花；若△PDC，△ADE，△CFB的面积分别为2m2，3 m2，5 m2且种植月季花。已知1 m2茉莉花的成本为120元，1 m2月季的成本为80元。试利用⑵中的结论求□DEFC的面积，并求美化后的总成本是多少元？
在△ABC中，∠BAC=90°，，AB=AC=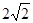
，圆的半径为1，如图所示，若点O在BC边上运动（与点B、C不重合），设OB=x，△AOC的面积为y.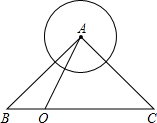
（1）求y关于x的函数解析式，并写出自变量的取值范围；
（2）以点O为圆心，BO长为半径作圆，求当圆O与圆A相切时，△AOC的面积.
在元旦联欢会上，有一个开盒有奖的游戏，两只外观一样的盒子，一只装有奖品，一只
是空的，游戏规定：每人每次游戏时主持人先混合盒子再拿出来，参加游戏的同学随机打开其中一只，若
有奖品，就获得该奖品，若是空盒子，就表演一个节目．
（1）两个人参加游戏，都获奖的概率为_______．
（2）n个人参加游戏，全部获奖的概率为________．
（3）现取三只外观一样的盒子，一只内有奖品，另两只空盒子，游戏规则不变．两个人参加游戏，用画树形
图法求至少有一个人表演节目的概率．
如图，在△ABC和△ADE中，点E在BC上，∠B=∠D，AB=AD，∠EAC=∠DAB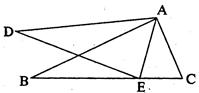
（1）求证：AE=AC.
（2）如果∠AEC=75°，将△ADE绕点A旋转一个锐角后，与△ABC重合，求这个旋转角的大小。
（3）在（2）的条件下，若AD=10，则D点所经过的路径长为________.
已知关于x的一元二次方程
.
①证明该方程有两个不相等实根；
②若该方程两根刚好是一直角三角形两直角边长，且该直角三角形斜边为10，求k值。
已知抛物线经过点A（－3，0）和点B（5，0）且抛物线的顶点纵坐标为6，求抛物线的解析式。