如图①，将一张直角三角形纸片ABC折叠，使点A与点C重合，这时DE为折痕，△CBE为等腰三角形，再继续将纸片沿△CBE的对称轴EF折叠，这时得到了两个完全重合的矩形（其中一个是原三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样的两个矩形为“叠加矩形”．请完成下列问题：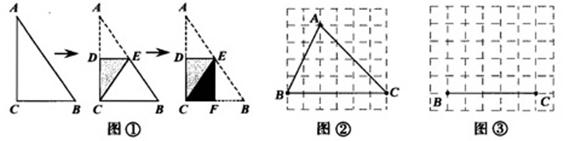
如图②，正方形网格中的△ABC能折叠成“叠加矩形”吗？如能，请在图②中画出折痕；
如图③，在正方形网格中，以给定的BC为一边，画出一个斜△ABC，使其顶点A在格点上，且△ABC折成的“叠加矩形”为正方形；
如果一个三角形所折成的“叠加矩形” 为正方形，那么它必须满足的条件是 ．
如图是某货站传送货物的平面示意图，AD与地面的夹角为60°，为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°变成37°，因此传送带的落地点由点B到点C向前移动了2米.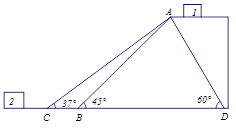
（1）求点A与地面的高度；
（2）如果需要在货物着地点C的左侧留出2米，那么请判断距离D点14米的货物2是否需要挪走，并说明理由.（sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，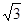
≈1.73）
某建设工程准备招标，指挥部现接到甲、乙两个工程队的投标书，从投标书中得知：乙队单独完成这项工程所需天数是甲队单独完成这项工程所需天数的2倍；该工程若由甲队先做6天，剩下的工程再由甲、乙两队合作16天可以完成.
（1）求甲、乙两队单独完成这项工程各需要多少天？
（2）已知甲队每天的施工费用为0.67万元，乙队每天的施工费用为0.33万元，该工程预算的施工费用为19万元.为缩短工期，拟安排甲、乙两队同时开工合作完成这项工程，问：该工程预算的施工费用是否够用？若不够用，需要追加预算多少万元？请说明理由.
如图，在直角梯形ABCD中，AD∥BC，AB⊥AD，BC＝CD，BE⊥CD，垂足为E，点F在BD上，连接AF、EF．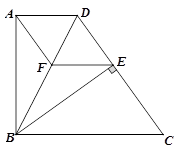
（1）求证：DA＝DE；
（2）如果AF∥CD，请判断四边形ADEF是什么特殊的四边形，并证明您的结论．
甲、乙两个袋中均装有三张除所标数值外完全相同的卡片，甲袋中的三张卡片上所标有的三个数值为﹣7，﹣1，3．乙袋中的三张卡片所标的数值为﹣2，1，6．先从甲袋中随机取出一张卡片，用x表示取出的卡片上的数值，再从乙袋中随机取出一张卡片，用y表示取出卡片上的数值，把x、y分别作为点A的横坐标和纵坐标．
（1）用适当的方法写出点A（x，y）的所有情况．
（2）求点A落在第一象限的概率．
学校以1班学生的地理测试成绩为样本，按A、B、C、D四个等级进行统计，并将统计结果绘制成两幅统计图，结合图中信息填空：
（1）D级学生的人数占全班人数的百分比为；
（2）扇形统计图中C级所在扇形圆心角度数为；
（3）该班学生地理测试成绩的中位数落在级内；
（4）若该校共有1500人，则估计该校地理成绩得A级的学生约有人．