已知数列{an}是公比q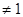 的等比数列,给出下列六个数列:(1){kan}(k
的等比数列,给出下列六个数列:(1){kan}(k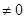 ) (2){a2n-1} (3){an+1-an} (4){anan+1} (5){nan} (6){an3},其中仍能构成等比数列的个数为()
) (2){a2n-1} (3){an+1-an} (4){anan+1} (5){nan} (6){an3},其中仍能构成等比数列的个数为()
| A.4 | B.5 | C.6 | D.3 |
若x,2x+2,3x+3是一个等比数列的连续三项,则x的值为()
| A.-4 | B.-1 | C.1或4 | D.-1或-4 |
在2与6之间插入n个数,使它们组成等比数列,则这个数列的公比为()
A. |
B.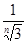 |
C.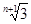 |
D.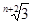 |
在等比数列{an}中,a9+a10=a(a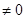 ),a19+a20=b,则a99+a20的值为()
),a19+a20=b,则a99+a20的值为()
A. |
B.(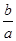 )9 )9 |
C.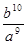 |
D.(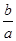 )10 )10 |
若数列{an}是等比数列,公比为q,则下列命题中是真命题的是()
A.若q>1,则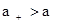 |
B.若0<q<1,则an+1<an |
| C.若q=1,则sn+1=Sn | D.若-1<q<0,则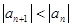 |