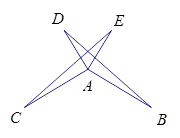
如图,已知BE⊥AD交AD延长线于点E,CF⊥AD于点F,且BE=CF.请你判断AD是△ABC的中线还是角平分线?说明理由.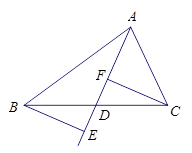
如图,在△ABC中,AB<AC,DE是BC边的垂直平分线,DE交BC于D点,交AC于点E,AC=8㎝,△ABE的周长是14㎝,求AB的长度.
一艘轮船从港口A出发,以10海里/时的速度向正北航行,从港口A处测得一礁石C在北偏西30°方向上,若这艘船上午8:00从港口A出发10:00到达小岛B,此时在小岛B测得礁石在北偏西60°方向上.(1)画出礁石的位置;(2)求出小岛B距礁石C多远.
一个三角形两个角的度数是方程组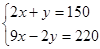 的解,试判断该三角形的形状.
的解,试判断该三角形的形状.
如图,已知AE⊥AB,AD⊥AC,AB=AC,∠B=∠C,求证:BD=CE