如图,在平面直角坐标系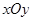 中,已知二次函数
中,已知二次函数 的图像与
的图像与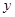 轴交于点
轴交于点 ,与
,与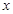 轴交于A、B两点,点B的坐标为
轴交于A、B两点,点B的坐标为
求二次函数的解析式及顶点D的坐标;
点M是第二象限内抛物线上的一动点,若直线OM把四边形ACDB分成面积为1:2的两部分,求出此时点
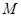 的坐标;
的坐标;点P是第二象限内抛物线上的一动点,问:点P在何处时△
 的面积最大?最大面积是多少?并求出 此时点P的坐标.
的面积最大?最大面积是多少?并求出 此时点P的坐标.
如图,在正方形ABCD中,以AD为边作等边三角形ADE,点E在正方形内部,将AB绕着点A顺时针旋转30°得到线段AF,连结EF.求证:四边形ADEF是菱形.
我国从2011年1月1日起在公共场所实行“禁烟”,到2015年1月1日,实行了四年.某社区为进一步巩固“禁烟”成果,开展了“你支持哪种戒烟方式”的问卷调查,随机抽样调查了该社区部分居民的意见,并将调查结果整理后绘制成如下统计图.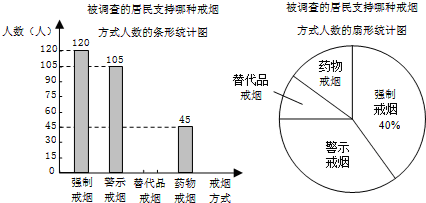
(1)该社区一共随机调查了多少人;
(2)此次抽样调查的居民中,支持“替代品戒烟”的居民有人,并补全条形统计图;
(3)若该社区共有居民18000人,则该社区大约有多少人支持“警示戒烟”这种方式.
如图,甲楼AB的高度为35m,经测得,甲楼的底端B处与乙楼的底端D处相距105m,从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为25°.求乙楼CD的高度(结果精确到0.1m).[参考数据:sin25°=0.42,cos25°=0.91,tan25°=0.47].
某市为了在冬季下雪时更好的清扫路面积雪,新购进一批清雪车.每辆新清雪车比每辆旧清雪车每小时多清扫路面2km,每辆新清雪车清扫路面35km与每辆旧清雪车清扫路面25km所用的时间相同,求每辆旧清雪车每小时清扫路面多少km?
甲、乙两个不透明的口袋中各装有3个小球,它们除所标数字不同外其余均相同.甲口袋中小球分别标有数字1,5,7,乙口袋中小球分别标有数字0,1,2.现从甲口袋中随机摸出1个小球,记下标号;再从乙口袋中随机摸出1个小球,记下标号.用画树状图(或列表)的方法,求两次摸出小球的标号之和是偶数的概率.