已知:如图,在平面直角坐标系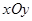 中,矩形OABC的边OA在
中,矩形OABC的边OA在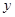 轴的正半轴上,OC在
轴的正半轴上,OC在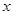 轴的正半轴上,OA=2,OC=3。过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E。
轴的正半轴上,OA=2,OC=3。过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E。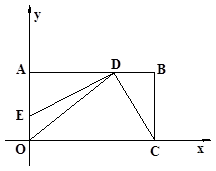
(1)求过点E、D、C的抛物线的解析式;
(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与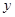 轴的正半轴交于点F,另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M,点M的横坐标为
轴的正半轴交于点F,另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M,点M的横坐标为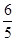 ,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由。
(·辽宁辽阳)如图1,平面直角坐标系中,直线 与抛物线
与抛物线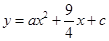 相交于A,B两点,其中点A在x轴上,点B在y轴上.
相交于A,B两点,其中点A在x轴上,点B在y轴上.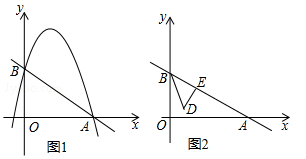
(1)求抛物线的解析式;
(2)在抛物线上存在一点M,使△MAB是以AB为直角边的直角三角形,求点M的坐标;
(3)如图2,点E为线段AB上一点,BE=2,以BE为腰作等腰Rt△BDE,使它与△AOB在直线AB的同侧,∠BED=90°,△BDE沿着BA方向以每秒一个单位的速度运动,当点B与A重合时停止运动,设运动时间为t秒,△BDE与△AOB重叠部分的面积为S,直接写出S关于t的函数关系式,并写出自变量t的取值范围.
(·辽宁辽阳)菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是 ;
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且 时,直接写出线段CE的长.
时,直接写出线段CE的长.
如图,抛物线 交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且 ,求点P的坐标;
,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.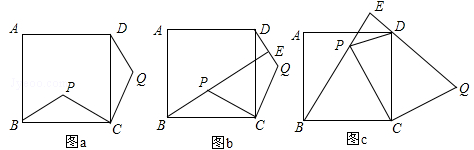
(1)如图a,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.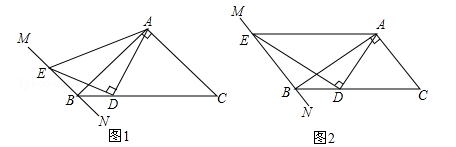
(1)如图①,当∠ABC=45°时,求证:AD=DE;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)