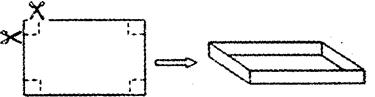
如图,把…张长10cm,宽8cm的矩形硬纸枥的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).要使长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
你感到折合而成的长方体盒子的侧面积(不含底面)会不会有最大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由
某校为了选拔省教委组织的以“爱我省会•让节能环保称为时尚”为主题的参赛作品,现在本校组织了一次“以爱我家乡•让节能环保成为时尚”的作品征集活动,现从所收集上来的作品中随机爱抽取了一部分,按A,B,C,D四个等级进行评选,并根据评选结果绘制了如图所示的条形统计图,已知等级C的作品的所抽取作品中占25%.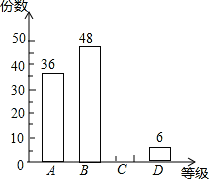
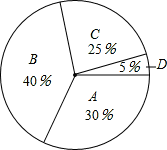
(1)求所抽取的作品的总份数及等级C的作品的份数,并补全条形统计图;
(2)若该校供征集到800份作品.
①请你估计出等级为A的作品约有多少份?
②若等级为A的作品中有100份是七年级组的作品,剩下的为八、九年级组的作品,现要将这两个组的作品再进行分组来选择参赛用的作品,已知这两个组所分的组数相同,且七年级组中每组的作品比八、九年级组中每组的作品少4份,请问这两个年级组的作品中每组各多少份?
已知△ABC中的∠A与∠B满足(1-tanA)2+|sinB- |=0
|=0
(1)试判断△ABC的形状.
(2)求(1+sinA)2-2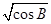 -(3+tanC)0的值.
-(3+tanC)0的值.
已知:如图①,在矩形ABCD中,AB=5,AD= ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值.
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
某电器超市销售每台进价分别为200元,170元的A、B联众型号的电风扇,表中是近两周的销售情况:
| 销售时段 |
销售数量 |
销售收入 |
|
| A种型号 |
B种型号 |
||
| 第一周 |
3台 |
5台 |
1800元 |
| 第二周 |
4台 |
10台 |
3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
已知抛物线C:y=-x2+bx+c经过A(-3,0)和B(0,3)两点,将这条抛物线的顶点记为M,它的对称轴与x轴的交点记为N.
(1)求抛物线C的表达式;
(2)求点M的坐标;
(3)将抛物线C平移到抛物线C′,抛物线C′的顶点记为M′,它的对称轴与x轴的交点记为N′.如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形,那么应将抛物线C怎样平移?为什么?