在三张完全相同的卡片上分别标注:A“雨水”、B“大地”、C“生机”,放入一个不透明的的口袋中,随机从中抽出一张放入“ 给
给 带来
带来 ”左边“
”左边“ ”内;第二次抽出一张放入中间的“
”内;第二次抽出一张放入中间的“ ”内;第三次抽出一张放入右边的“
”内;第三次抽出一张放入右边的“ ”内(每次卡片抽出后不放回).
”内(每次卡片抽出后不放回).试用树形图列出三次抽卡出现的所有可能的结果;
求其中恰好组成“雨水给大地带来生机”的概率.
已知关于x的一元二次方程x2+x+m2﹣2m=0有一个实数根为﹣1,求m的值及方程的另一实根.
中央电视台举办的“中国汉字听写大会”节目受到中学生的广泛关注.某中学为了了解学生对观看“中国汉字听写大会”节目的喜爱程度,对该校部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图.在条形图中,从左向右依次为A类(非常喜欢),B类(较喜欢),C类(一般),D类(不喜欢).已知A类和B类所占人数的比是5:9,请结合两幅统计图,回答下列问题: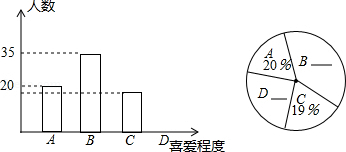
(1)写出本次抽样调查的样本容量;
(2)请补全两幅统计图;
(3)若该校有2000名学生.请你估计观看“中国汉字听写大会”节目不喜欢的学生人数.
先化简,再求值: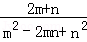 •(m﹣n),其中
•(m﹣n),其中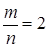 .
.
如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线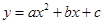 (
( )过E,A′两点.
)过E,A′两点.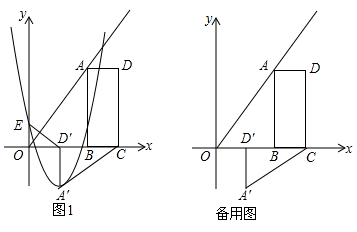
(1)填空:∠AOB=°,用m表示点A′的坐标:A′(,);
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且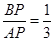 时,△D′OE与△ABC是否相似?说明理由;
时,△D′OE与△ABC是否相似?说明理由;
(3)若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.
如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.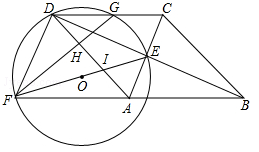
(1)求∠FDE的度数;
(2)试判断四边形FACD的形状,并证明你的结论;
(3)当G为线段DC的中点时,
①求证:FD=FI;
②设AC=2m,BD=2n,求⊙O的面积与菱形ABCD的面积之比.