一个袋子中有5个大小相同的球,其中3个白球与2个黑球,现从袋中任意取出一个球,取出后不放回,然后再从袋中任意取出一个球,求第一次为白球第二次为黑球的概率为( )
A.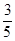 |
B.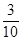 |
C.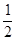 |
D.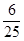 |
已知命题p: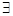
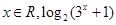 ≤0,则( )
≤0,则( )
A.p是假命题;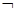 p: p: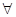 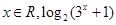 ≤0 ≤0 |
B.p是假命题;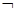 p: p: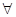 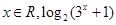 >0 >0 |
C.p是真命题;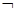 p: p: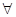 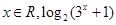 ≤0 ≤0 |
D.p是真命题;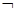 p: p: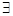 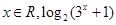 >0 >0 |
已知集合A={x|x2+x-2<0},集合B={x|(x+2)(3-x)>0},则 等于( )
等于( )
| A.{x|1≤x<3} | B.{x|2≤x<3} |
| C.{x|-2<x<1} | D.{x|-2<x≤-1或2≤x<3} |
设a,b,c,d∈(0,+∞),若a+d=b+c且|a-d|<|b-c|,则有( )
| A.ad=bc | B.ad<bc |
| C.ad>bc | D.ad≤bc |
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
| A.假设三个内角都不大于60度 |
| B.假设三个内角都大于60度 |
| C.假设三个内角至多有一个大于60度 |
| D.假设三个内角有两个大于60度 |
如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,那么( )
| A.△A1B1C1和△A2B2C2都是锐角三角形 |
| B.△A1B1C1和△A2B2C2都是钝角三角形 |
| C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形 |
| D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形 |