图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.
(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′;
(2)△A′B′C′绕点B′顺时针旋转90°,画出旋转后得到的△A″ C″,并求边A′B′在旋转过程中扫过的图形面积.
C″,并求边A′B′在旋转过程中扫过的图形面积.
如图,AB是⊙O的直径,AM、BN分别切⊙O于点A、B,CD交AM,BN于点D、C,DO平分∠ADC.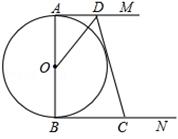
(1)求证:CD是⊙O的切线;
(2)若AD=4,BC=9,求⊙O的半径R.
已知:函数y=ax2﹣(3a+1)x+2a+1(a为常数).
(1)若该函数图象与坐标轴只有两个交点,求a的值;
(2)若该函数图象是开口向上的抛物线,与x轴相交于点A(x1,0),B(x2,0)两点,与y轴相交于点C,且x2﹣x1=2.
①求抛物线的解析式;
②作点A关于y轴的对称点D,连结BC,DC,求sin∠DCB的值.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1。
(1)求BD的长
(2)若△DCN的面积为2,求四边形ABNM的面积。
如图所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.
(1)当∠CED=60°时,求C、D两点间的距离;
(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1cm)
(3)设DG=xcm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1cm)(参考数据 ≈1.732)
≈1.732)