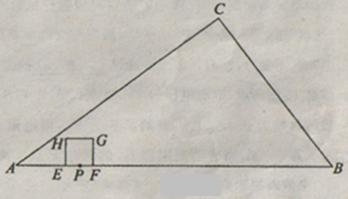
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立即以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分面积为S.当t=1时,正方形EFGH的边长是 ;
当t=3时,正方形EFGH的边长是 ;当0<t≤2时,求S与t的函数关系式;
直接答出:在整个运动过程中,当t为何值时,S最大?最大面积是多少?
在同一直角坐标系中画出下列函数的图象: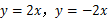 .
.
如图, ,
, ,∠
,∠ ,∠
,∠ ,求
,求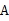 、
、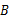 两点的坐标.
两点的坐标.
等腰梯形 的上底
的上底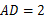 ,下底
,下底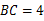 ,底角∠
,底角∠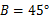 ,建立适当的直角坐标系,求各顶点的坐标.
,建立适当的直角坐标系,求各顶点的坐标.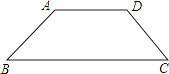
当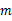 为何值时,(1)点
为何值时,(1)点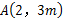 关于原点的对称点在第三象限;
关于原点的对称点在第三象限;
(2)点 到
到 轴的距离等于它到
轴的距离等于它到 轴距离的一半?
轴距离的一半?
四边形是大家最熟悉的图形之一,我们已经发现了它的许多性质.只要善于观察、乐于探索,我们还会发现更多的结论.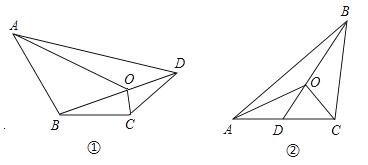
(1)四边形一条对角线上任意一点与另外两个顶点的连线,将四边形分成四个三角形(如图①),其中相对的两对三角形的面积之积相等.你能证明这个结论吗?试试看.
已知:在四边形ABCD中,O是对角线BD上任意一点(如图①);
求证: .
.
证明:
(2)在三角形中(如图②),你能否归纳出类似的结论?若能,写出你猜想的结论,并证明;若不能,请说明理由.