现代观测表明，由于引力作用，恒星有“聚集”的特点，.众多的恒星组成不同层次的恒星系统，最简单的恒星系统是两颗互相绕转的双星，如图所示，两星各以一定速率绕其连线上某一点匀速转动，这样才不至于因万有引力作用而吸引在一起，已知双星质量分别为m１、m2，它们间的距离始终为L，引力常数为G，求：
(1)双星旋转的中心O到m１的距离；
(2)双星的转动周期.
(10分)如图所示，半径为R的竖直环内侧凹槽光滑，AOB为一条水平直径。质量为m的小球（可视为质点）从A点以一定的速率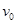
开始向上沿圆环凹槽运动，若要使小球刚好能在竖直环内侧凹槽内做圆周运动，求：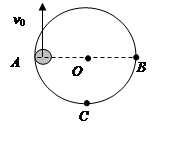
（1）小球从A点运动的初速度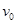的大小。
（2）小球到达圆环最低点C处时对凹槽的压力是多大？
(9分)如图，跳台滑雪运动员经过一段加速滑行后从O点水平飞出，经3.0s落到斜坡上的A点.已知O点是斜坡的起点，斜坡与水平面的夹角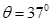
，运动员的质量m=50kg.不计空气阻力.（取
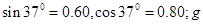取10m/s2）求
（1）A点与O点的距离L；
（2）运动员离开O点时的速度大小；
（3）运动员落到A点时的动能.
如图所示，质量为m=0.1kg的小球和A、B两根绳相连，两绳固定在细杆的A、B两点，其中A绳长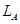
=2m，当两绳都拉直时，A、B两绳和细杆的夹角
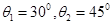，g=10m/s2。求
（1）细杆转动的角速度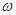
在什么范围内，A、B两绳始终张紧？
（2）当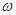=3rad/s时，A、B两绳的拉力分别为多大？
如图所示，质量均为m的小球A、B、C，用两根长为l的细线相连，置于高为h的光滑水平桌面上，
> h，A球刚跨过桌边。若A球、B球相继下落着地后均不再反跳，则C球离开桌边的速度多大？
额定功率为80kW的汽车在平直公路上行驶时，其最大速度可达20m/s，汽车的质量为2t。如果从静止开始做匀加速运动，设运动中阻力不变，加速度为2 m/s2，求
（1）汽车所受的阻力；
（2）这个匀加速运动过程能维持多长时间？
（3）第3s末汽车的瞬时功率。