1798年英国物理学家卡文迪许测出万有引力常量G,因此卡文迪许被人们称为能称出地球质量的人,若已知万有引力常量G,地球表面处的重力加速度g,地球半径为R,地球上一个昼夜的时间为T1(地球自转周期),一年的时间T2(地球公转的周期),地球中心到月球中心的距离L1,地球中心到太阳中心的距离为L2.你能计算出( )
A.地球的质量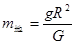 |
B.太阳的质量 |
C.月球的质量 |
D.可求月球、地球及太阳的密度 |
几个做匀变速直线运动的物体,在前t s内位移最大的是 ()
| A.加速度最大的物体 | B.初速度最大的物体 |
| C.末速度最大的物体 | D.平均速度最大的物体 |
如图所示,L1、L2是劲度系数均为k的轻质弹簧,A、B两只钩码重量均为G,则静止时两弹簧伸长量之和为()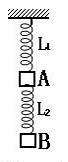
A.3G/k B.2G/k
C.G/k D.G/2k
两辆汽车速度相等,在同时制动后,设均做匀减速运动,甲经3s停止,共前进了36m,乙经1.5s停止,乙车前进的距离为()
| A.9m | B.18m | C.27m | D.36m |
从静止开始做匀加速直线运动的物体,在第1s内、第2s内、第3s内的平均速度之比为()
| A.1∶3∶5 | B.1∶4∶9 | C.1∶2∶3 | D.1∶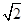 ∶ ∶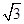 |
一辆以20m/s的速度在水平路面行驶的汽车,刹车过程中以大小为5m/s2的加速度作匀变速直线运动,则汽车在制动以后2S内与制动后6S内的位移之比是()
| A.1:1 | B.4:3 |
| C.3:1 | D.3:4 |