为了保证中小学学生上下学的安全,某县根据实际需要计划购买大、中型两种校车共20辆,已知大型校车每辆62万元,中型校车每辆40万元,设购买大型校车x(辆),购车总费用为y(万元).求y与x的函数关系式(不要求写出自变量x的取值范围);
若购买中型校车的数量少于大型校车的数量,请你给出一种费用最省的方案,
并求出该方案所需费用.
我校数学兴趣小组为了解美利达自行车的销售情况,对我市美利达专卖店第一季度 A、B、C、D四种型号的销量做了统计,绘制成如下两幅统计图(均不完整)。
(1) 该店第一季度售出美利达自行车共多少辆?
(2) 把两幅统计图补充完整;
(3) 若该专卖店计划订购这四款型号自行车900辆,求C型自行车应订购多少辆?
临近端午节,某食品店每天卖出300只粽子,卖出一只粽子的利润为1元..经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获得的利润更多,该店决定把零售单价下降m(0<m<1)元,
(1)零售单价降价后,该店每天可售出只粽子,利润为元。
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,且卖出的粽子更多?
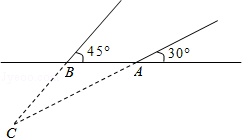
某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象.已知A、B两点相距6米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米,参考数据: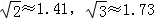 )
)
如图,每个大正方形是由边长为1的小正方形组成。观察以上图形,完成下列填空: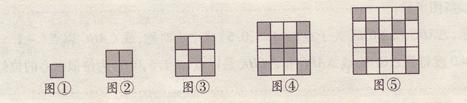
(1)猜想:当n为奇数时,图n中黑色小正方形的个数为,当n为偶数时,图n中黑色小正方形的个数为;
(2)在边长为偶数的正方形中,白色小正方形的个数是黑色小正方形个数的4倍,求这个正方形的边长。
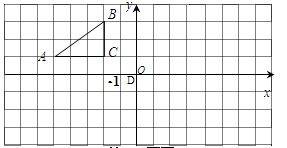
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-5,1),点B的坐标为(-3,3),点C的坐标为(-3,1)。
(1)将Rt△ABC沿x轴正方向平移7个单位得到Rt△A1B1C1,试在图上画出的图形Rt△A1B1C1的图形;
(2)Rt△ABC关于点D(-1,0)对称的图形是Rt△A2B2C2,试在图上画出Rt△A2B2C2的图形,并写出A2、B2、C2点的坐标。