如图①，以点M（－1,0）为圆心的圆与y轴、x轴分别交于点A、B、C、D，直线y＝－x－与⊙M相切于点H，交x轴于点E，交y轴于点F．请直接写出OE、⊙M的半径r、CH的长；
如图②，弦HQ交x轴于点P，且DP:PH＝3:2，求cos∠QHC的值；
如图③，点K为线段EC上一动点（不与E、C重合），连接BK交⊙M于点T，弦AT交x轴于点N．是否存在一个常数a，始终满足MN·MK＝a，如果存在，请求出a的值；如果不存在，请说明理由．
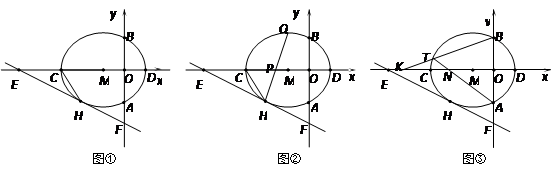
如图，A，B是⊙O上的两个定点，P是⊙O上的动点（P不与A，B重合），我们称∠APB是⊙O上关于A、B的滑动角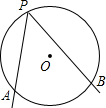
（1）已知∠APB是⊙O上关于点A、B的滑动角，
①若AB是⊙O的直径，则∠APB=°；
②若⊙O的半径是1，AB=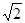
，求∠APB的度数；
（2）已知O2是⊙O1外一点，以O2为圆心作一个圆与⊙O1相交于A、B两点，∠APB是⊙O1上关于点A、B的滑动角，直线PA、PB分别交⊙O2于M、N（点M与点A、点N与点B均不重合），连接AN，试探索∠APB与∠MAN、∠ANB之间的数量关系，直接写出结论．
观察图形，解答问题：
（1）按下表已填写的形式填写表中的空格：
| 图① |
图② |
图③ |
|
| 三个角上三个数的积 |
1×（-1）×2=-2 |
（-3）×（-4）×（-5）=-60 |
|
| 三个角上三个数的和 |
1+（-1）+2=2 |
（-3）+（-4）+（-5）=-12 |
|
| 积与和的商 |
-2÷2=-1， |
请用你发现的规律求出图④中的数y和图⑤中的数x．
如图，在△ABC中，AB=AC，∠B=30°，BC=8，D在边BC上，E在线段DC上，DE=4，△DEF是等边三角形，边DF交边AB于点M，边EF交边AC于点N．
（1）求证：△BMD∽△CNE；
（2）当BD为何值时，以M为圆心，以MF为半径的圆与BC相切？
（3）设BD=x，五边形ANEDM的面积为y，求y与x之间的函数解析式及自变量x的取值范围；当x为何值时，y有最大值？并求出y的最大值．
某童装厂现有甲种布料38米，乙种布料26米，现计划用这两种布料生产L、M两种型号的童装共50套.已知做一套L型号的童装需用甲种布料0.5米，乙种布料1米，可获利45元；做一套M型号童装需用甲种布料0.9米，乙种布料0.2米，可获利30元，设生产L型号的童装套数为x，用这批布料生产这两种型号的童装所获的利润为y(元).
(1)如果你作为该厂的老板，应如何安排生产计划？请设计出所有生产方案；
(2)该厂在生产这批童装中，当L型号的童装为多少套时，能使该厂所获的利润最大?最大利润为多少?
（1）比较下列算式结果的大小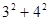
；
；
；
；
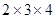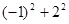
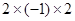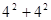
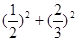
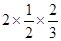（2）观察以上各式所反映的规律，用一个含字母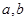
的式子表示出来；
（3）若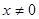
，求
的最小值；
（4）若
是正数，则
的最小值为。