如图,正方形网格中,每一个小正方形的边长都是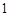 ,四边形
,四边形 的四个顶点都在格点上,
的四个顶点都在格点上, 为
为 边的中点,若把四边形
边的中点,若把四边形 绕着点
绕着点 顺时针旋转
顺时针旋转 .
.画出四边形
 旋转后的图形;
旋转后的图形;设点
 旋转后的对应点为
旋转后的对应点为 ,则
,则 ;
;求点
 在旋转过程中所经过的路径长.
在旋转过程中所经过的路径长.
已知点A在数轴上对应的数为a,点B对应的数为b,且|a+4|+(b﹣3)2=0,
(1)则a= ,b= ;并将这两数在数轴上所对应的点A、B表示出来;
(2)数轴上在B点右边有一点C到A、B两点的距离和为11,求点C在数轴上所对应的数;
(3)若A点,B点同时沿数轴向正方向运动.点A的速度是点B的2倍,且3秒后,2OA=OB,求点B的速度.
友情提示:M、N之间距离记作 ,点M、N在数轴上对应的数分别为m、n,则
,点M、N在数轴上对应的数分别为m、n,则 .
.
一列火车匀速行驶,经过一条长300米的隧道需要20s的时间,隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10s.
(1)设火车的长为xm,用含x的式子表示:从火车头经过灯下到车尾经过灯下火车所走的路程是______;这段时间火车的平均速度是________;
(2)求这列火车的长度.
列方程解应用题:
(1)某车间32名工人生产螺母和螺钉,每人每天平均生产螺钉1500个或螺母5000个,一个螺钉要配两个螺母,为了使每天的产品刚好配套,应该分配多少名工人生产螺钉?
(2)一艘船从甲码头到乙码头顺流行驶用4小时,从乙码头到甲码头逆流行驶用4小时40分钟,已知水流速度为3千米/小时,则船在静水中的平均速度是多少?
“囧”(jiǒng)曾经是一个风靡网络的流行词,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
(1)用含有x、y的代数式表示右图中“囧”(阴影部分)的面积;
(2)当x=2y=8时,求此时“囧”的面积;
某村小麦种植面积是a公顷,水稻种植面积比小麦种植面积的2倍还多25公顷,玉米的种植面积比小麦种植面积少5公顷,列式计算水稻种植面积比玉米种植面积大多少公顷?