一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式。比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.图③可以解释为等式:
在虚线框中用图①中的基本图形拼成若干块(每种至少用一次)拼成一个矩形,使拼出的矩形面积为2a2+7ab+3b2,并标出此矩形的长和宽.
如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式
(1)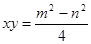 (2)
(2)
(3)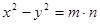 (4)
(4)
其中正确的有几个……………………………… ( )
| A.1个 | B.2个 | C.3个 | D.4个 |

如图,一条直线与反比例函数 的图象交于A(1,4).B(4,n)两点,与
的图象交于A(1,4).B(4,n)两点,与 轴交于D点,AC⊥
轴交于D点,AC⊥ 轴,垂足为C.
轴,垂足为C.如图甲,①求反比例函数的解析式;②求n的值及D点坐标.
如图乙,若点E在线段AD上运动,连结CE,作∠CEF=45°,EF交AC于F点.
①试说明△CDE∽△EAF的理由.
②当△ECF为等腰三角形时,直接写出F点坐标. 
先阅读下面解方程 的过程,然后回答后面的问题。
的过程,然后回答后面的问题。
解:将原方程整理为: (第一步)
(第一步)
方程两边同除以(x-1)得: 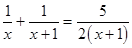 (第二步)
(第二步)
去分母,得:2(x+1)+2x=5x(第三步)
解这个方程,得:x=2(第四步)
在上面的解题过程中:第三步变形的依据是
出现错误的一步是
上述解题过程缺少的一步是
写出这个方程的完整的解题过程
如图:已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与A、C不重合),Q在BC上.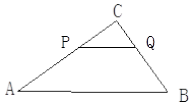
当△PQC的面积是四边形PABQ的面积
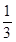 时,求CP的长
时,求CP的长当△PQC的周长与四边形PABQ的周长相等时,求CP的长.
如图,△ABC在方格纸中请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
以原点O为位似中心,位似比为2,在第一象限内将△ABC放大,画出放大后的位似图形
 ;
;计算
 的面积S.
的面积S. 
如图,在△ABC中,点D、E分别在AB和AC上,且DE∥BC,AD∶DB=3∶2, ,求四边形BCED的面积.
,求四边形BCED的面积.