某单位招聘面试,每次从试题库随机调用一道试题,若调用的是类型试题,则使用后该试题回库,并增补一道 类试题和一道
类试题和一道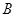 类型试题入库,此次调题工作结束;若调用的是类型试题,则使用后该试题回库,此次调题工作结束。试题库中现共有道试题,其中有道类型试题和道类型试题,以表示两次调题工作完成后,试题库中类试题的数量。
类型试题入库,此次调题工作结束;若调用的是类型试题,则使用后该试题回库,此次调题工作结束。试题库中现共有道试题,其中有道类型试题和道类型试题,以表示两次调题工作完成后,试题库中类试题的数量。
(Ⅰ)求的概率;
(Ⅱ)设,求的分布列和均值(数学期望)。
如图,中心在坐标原点,焦点分别在 轴和
轴和 轴上的椭圆
轴上的椭圆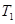 ,
, 都过点
都过点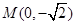 ,且椭圆
,且椭圆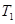 与
与 的离心率均为
的离心率均为 .
.
(Ⅰ)求椭圆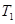 与椭圆
与椭圆 的标准方程;
的标准方程;
(Ⅱ)过点 引两条斜率分别为
引两条斜率分别为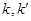 的直线分别交
的直线分别交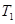 ,
, 于点P,Q,当
于点P,Q,当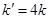 时,问直线PQ是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
时,问直线PQ是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
已知数列{an}中, .
.
(Ⅰ)求证:数列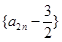 是等比数列;
是等比数列;
(Ⅱ)设 是数列
是数列 的前
的前 项和,求满足
项和,求满足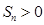 的所有正整数
的所有正整数 .
.
已知四棱锥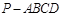 中,底面ABCD为
中,底面ABCD为 的菱形,
的菱形,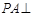 平面ABCD,点Q在直线PA上.
平面ABCD,点Q在直线PA上.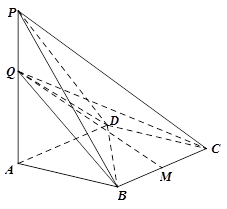
(Ⅰ)证明:直线QC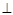 直线BD;
直线BD;
(Ⅱ)若二面角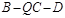 的大小为
的大小为 ,点M为BC的中点,求直线QM与AB所成角的余弦值.
,点M为BC的中点,求直线QM与AB所成角的余弦值.
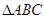 中,内角
中,内角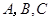 的对边分别是
的对边分别是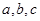 ,已知
,已知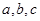 成等比数列,且
成等比数列,且 .
.
(Ⅰ)求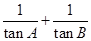 的值;
的值;
(Ⅱ)设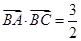 ,求
,求 的值.
的值.
已知函数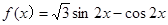 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)求函数 的单调递减区间;
的单调递减区间;
(Ⅲ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.