甲、乙两个篮球队进行比赛,比赛采用5局3胜制(即先胜3局者获胜).若甲、乙两队在每场比赛中获胜的概率分别为 和
和 ,记需要比赛的场次为
,记需要比赛的场次为 ,则
,则 = .
= .
在棱长为3的正四面体ABCD中,点E是线段AB上一点,且AE="1," 点F是线段AD上一点,且AF=2,则异面直线DE与CF的夹角的余弦为.
已知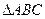 的三个内角
的三个内角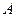 、
、 、
、 成等差数列,且
成等差数列,且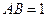 ,
,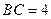 ,则边
,则边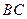 上的中线
上的中线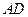 的长为.
的长为.
给出下列命题:
①若椭圆长轴长与短轴长的和为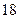 ,焦距为
,焦距为 ,则椭圆的标准方程为
,则椭圆的标准方程为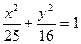 ;
;
②曲线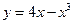 在点
在点 处的切线方程是
处的切线方程是 ;
;
③命题“若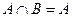 ,则
,则 ”的逆否命题是:“若
”的逆否命题是:“若 ,则
,则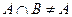 ”;
”;
④高台跳水运动员在 秒时距水面高度
秒时距水面高度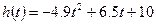 (单位:米),则该运动员的初速度为
(单位:米),则该运动员的初速度为 (米/秒);
(米/秒);
⑤“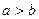 ”是“
”是“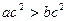 ”的充分条件。
”的充分条件。
正确的命题是。
若 是过圆锥曲线中心的任一条弦,
是过圆锥曲线中心的任一条弦,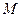 是二次曲线上异于
是二次曲线上异于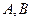 的任一点,且
的任一点,且 均与坐标轴不平行,则对于椭圆
均与坐标轴不平行,则对于椭圆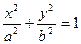 ,有
,有 ,类似的,对于双曲线
,类似的,对于双曲线 ,有
,有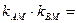 。
。
以双曲线 的离心率为半径,右焦点为圆心的圆与双曲线的一条渐近线相切,则
的离心率为半径,右焦点为圆心的圆与双曲线的一条渐近线相切,则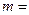 。
。