为了加强食品安全管理,有关部门对某大型超市的甲乙两种品牌食用油共抽取20瓶进行检测,检测结果分成“优秀”,“合格”,“不合格”三个等级,数据处理后制成以下折线统计图和扇形统计图
⑴甲乙两种品牌食用油各被抽取了多少瓶用于检测?
⑵在该超市购买一瓶甲品牌食用油,请估计能买到“优秀”等级的概率是多少?
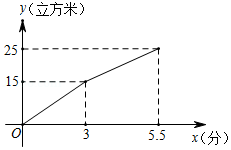
某种水泥储存罐的容量为25立方米,它有一个输入口和一个输出口.从某时刻开始,只打开输入口,匀速向储存罐内注入水泥,3分钟后,再打开输出口,匀速向运输车输出水泥,又经过2.5分钟储存罐注满,关闭输入口,保持原来的输出速度继续向运输车输出水泥,当输出的水泥总量达到8立方米时,关闭输出口.储存罐内的水泥量 (立方米)与时间 (分 之间的部分函数图象如图所示.
(1)求每分钟向储存罐内注入的水泥量.
(2)当 时,求 与 之间的函数关系式.
(3)储存罐每分钟向运输车输出的水泥量是 立方米,从打开输入口到关闭输出口共用的时间为 分钟.
某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
|
20 |
21 |
19 |
16 |
27 |
18 |
31 |
29 |
21 |
22 |
|
25 |
20 |
19 |
22 |
35 |
33 |
19 |
17 |
18 |
29 |
|
18 |
35 |
22 |
15 |
18 |
18 |
31 |
31 |
19 |
22 |
整理上面数据,得到条形统计图:
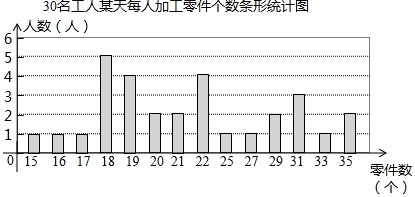
样本数据的平均数、众数、中位数如表所示:
|
统计量 |
平均数 |
众数 |
中位数 |
|
数值 |
23 |
|
21 |
根据以上信息,解答下列问题:
(1)上表中众数 的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
如图, 是 的直径, 切 于点 , 交 于点 .已知 的半径为6, .
(1)求 的度数.
(2)求 的长.(结果保留

学校准备添置一批课桌椅,原计划订购60套,每套100元,店方表示:如果多购,可以优惠.结果校方实际订购了72套,每套减价3元,但商店获得了同样多的利润.
(1)求每套课桌椅的成本;
(2)求商店获得的利润.
图①、图②均是 的正方形网格,每个小正方形的顶点称为格点,线段 、 的端点均在格点上.在图①、图②给定的网格中以 、 为邻边各画一个四边形,使第四个顶点在格点上.要求:
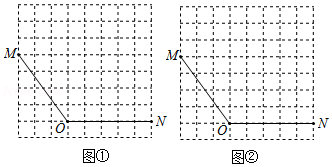
(1)所画的两个四边形均是轴对称图形.
(2)所画的两个四边形不全等.