如图，在直角坐标系xoy中，O是坐标原点，点A在x正半轴上，OA=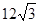
cm，点B在y轴的正半轴上，OB=12cm，动点P从点A开始沿AO以
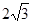cm/s的速度向点O移动，移动时间为t s(0＜t＜6).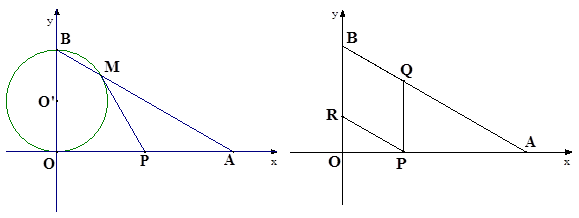
(1)求∠OAB的度数. (2分)
(2)以OB为直径的⊙O‘与AB交于点M，当t为何值时， PM与⊙O‘相切？
(3分)(3)动点Q从点A开始沿AB以4cm/s的速度向点B移动，动点R从点B开始沿BO以2cm/s的速度向点O移动. 如果P、Q、R分别从A、A、B同时移动，当t="4" s时，试说明四边形BRPQ为菱形；(3分)
(4)在(3)的条件下，以R为圆心，r为半径作⊙R，当r不断变化时，⊙R与菱形BRPQ各边的交点个数将发生变化，随当交点个数发生变化时，请直接写出r的对应值或取值范围．(4分)
某楼盘准备以每平方米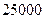
元的均价对外销售，由于国务院有关房地产的新政策出台，购房者持币观望．为了加快资金周转，房地产开发商对价格进行两次下调，最终以每平方米
元的均价开盘销售．
（1）求平均每次下调的百分率；
（2）某人准备以每平方米元的均价购买一套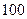
平方米的房子．开发商还给予以下两种优惠方案以供选择：①一次付清全款打九九折；②一次付清全款不打折，送五年物业管理费．如该楼盘物业管理费是每月
元/米2．请问哪种方案更优惠？
( 10分)如图，在平面直角坐标系中，Rt△OAB的直角边OA在x轴的正半轴上，点B在第象限，将△OAB绕点O按逆时针方向旋转至△OA′B′，使点B的对应点B′落在y轴的正半轴上，已知OB=2，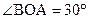
(1)求点B和点A′的坐标；
(2)求经过点B和点B′的直线所对应的一次函数解析式，并判断点A是否在直线BB′上。
已知：如图，四边形
是矩形，
和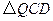
都是等边三角形，且点
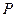在矩形上方，点
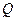在矩形内．
（1） 求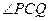
的度数；
（2） 求证：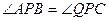
．
（本题11分）如图，已知二次函数的图象经过点A（3，3）、B（4，0）和原点O．
为二次函数图象上的一个动点，过点P作
轴的垂线，垂足为D（m，0），并与直线OA交于点C．
⑴ 求出二次函数的解析式；
⑵ 当点P在直线OA的上方时，求线段PC的最大值．
⑶ 当
时，探索是否存在点，使得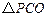
为等腰三角形，如果存在，求出的坐标；如果不存在，请说明理由．
（本题10分）如图，梯形ABCD中，AD∥BC，BC=2AD，F、G分别为边BC、CD的中点，连接AF，FG，过D作DE∥GF交AF于点E。
（1）证明△AED≌△CGF
（2）若梯形ABCD为直角梯形，判断四边形DEFG是什么特殊四边形？并证明你的结论。
 |