已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响。
(1)推导第一宇宙速度v1的表达式;
(2)若卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h,求卫星的运行周期T。
如图所示,光滑水平面上停着一个质量为M的木块乙,乙上固定着一轻质弹簧,另一个质量为m的木块以速度为 向右运动,求弹簧在压缩过程中所具有的最大弹性势能(设压缩量在弹性限度内)。
向右运动,求弹簧在压缩过程中所具有的最大弹性势能(设压缩量在弹性限度内)。

如图所示,从AB面射到矩形玻璃砖ABCD的光线,不论入射角i多大,都只能从CD面射出.求玻璃的折射率n的取值范围.
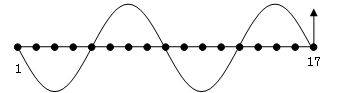
在水平线上有17个质点,每相邻两个质点间距离为4cm,如图所示.有一简谐波在该水平线上传播.已知第5个质点完成一次全振动经过的路程为8cm,时间为2s,当它从平衡位置开始向上振动通过12cm的路程时,第17个质点即将振动,求:
(1)该列波的传播速度。
(2)在图中画出第17个质点即将振动时的波形图,并标出第17个质点的振动方向。
如图所示,两物块M、N的质量分别为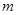 和
和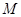 ,用劲度系数为
,用劲度系数为 的足够长的轻弹簧连在一起,放在水平面上,整个系统处于静止状态,现将木块M缓慢下压一端距离
的足够长的轻弹簧连在一起,放在水平面上,整个系统处于静止状态,现将木块M缓慢下压一端距离 后突然释放M,它就上下振动,在振动过程中木块N始终没有离开地面,弹簧的形变量在弹性限度内,求下压距离
后突然释放M,它就上下振动,在振动过程中木块N始终没有离开地面,弹簧的形变量在弹性限度内,求下压距离 的最大值。
的最大值。
两个星球组成双星,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动。现测得两星中心距离为R,其运动周期为T,求两星的总质量。