如图，△ABC内接于⊙O，CACB，CD∥AB且与OA的延长-优题课

一个不透明的口袋中有三个完全相同的小球，把他们分别标号为1，2，3．随机摸取一个小球然后放回，再随机摸出一个小球．用列表或画树状图的方法，求两次取出的小球标号相同的概率．

结果如此巧合 $!$

下面是小颖对一道题目的解答．

题目：如图， $Rt Δ ABC$ 的内切圆与斜边 $AB$ 相切于点 $D$ ， $AD = 3$ ， $BD = 4$ ，求 $ΔABC$ 的面积．

解：设 $ΔABC$ 的内切圆分别与 $AC$ 、 $BC$ 相切于点 $E$ 、 $F$ ， $CE$ 的长为 $x$ ．

根据切线长定理，得 $AE = AD = 3$ ， $BF = BD = 4$ ， $CF = CE = x$ ．

根据勾股定理，得 ${(x + 3)}^{2} + {(x + 4)}^{2} = {(3 + 4)}^{2}$ ．

整理，得 $x^{2} + 7 x = 12$ ．

所以 $S_{ΔABC} = \frac{1}{2} AC \cdot BC$

$= \frac{1}{2} (x + 3) (x + 4)$

$= \frac{1}{2} (x^{2} + 7 x + 12)$

$= \frac{1}{2} \times (12 + 12)$

$= 12$ ．

小颖发现12恰好就是 $3 \times 4$ ，即 $ΔABC$ 的面积等于 $AD$ 与 $BD$ 的积．这仅仅是巧合吗？

请你帮她完成下面的探索．

已知： $ΔABC$ 的内切圆与 $AB$ 相切于点 $D$ ， $AD = m$ ， $BD = n$ ．

可以一般化吗？

（1）若 $∠ C = 90 °$ ，求证： $ΔABC$ 的面积等于 $mn$ ．

倒过来思考呢？

（2）若 $AC \cdot BC = 2 mn$ ，求证 $∠ C = 90 °$ ．

改变一下条件 $\dots \dots$

（3）若 $∠ C = 60 °$ ，用 $m$ 、 $n$ 表示 $ΔABC$ 的面积．

如图，在正方形 $ABCD$ 中， $E$ 是 $AB$ 上一点，连接 $DE$ ．过点 $A$ 作 $AF ⊥ DE$ ，垂足为 $F$ ， $⊙ O$ 经过点 $C$ 、 $D$ 、 $F$ ，与 $AD$ 相交于点 $G$ ．

（1）求证： $ΔAFG ∽ ΔDFC$ ；

（2）若正方形 $ABCD$ 的边长为4， $AE = 1$ ，求 $⊙ O$ 的半径．

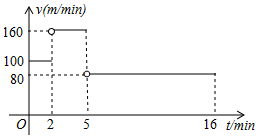
小明从家出发，沿一条直道跑步，经过一段时间原路返回，刚好在第 $16 \min$ 回到家中．设小明出发第 $tmin$ 时的速度为 $vm / \min$ ，离家的距离为 $sm$ ， $v$ 与 $t$ 之间的函数关系如图所示（图中的空心圈表示不包含这一点）．

（1）小明出发第 $2 \min$ 时离家的距离为　　 $m$ ；

（2）当 $2 < t ⩽ 5$ 时，求 $s$ 与 $t$ 之间的函数表达式；

（3）画出 $s$ 与 $t$ 之间的函数图象．

已知二次函数 $y = 2 (x - 1) (x - m - 3) (m$ 为常数）．

（1）求证：不论 $m$ 为何值，该函数的图象与 $x$ 轴总有公共点；

（2）当 $m$ 取什么值时，该函数的图象与 $y$ 轴的交点在 $x$ 轴的上方？