在密码学中，直接可以看到的内容为明码，对明码进行某种处理后得到的内容为密码。有一种密码，将英文的26个字母a,b,c……z（不论大小写）依次对应1,2,3……26这26个自然数（见表格）。当明码对应的序号x为奇数时，密码对应的序号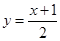
；当明码对应的序号x为偶数时，密码对应的序号为
。
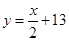| 字母 |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
| 序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| 字母 |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
| 序号 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
按上述规定，将明码“love”译成的密码是（ ）
A．gawq B．shxc C．sdri D．love
的相反数是（）
| A． |
B．5 | C．-5 | D．－ |
（2011湖南衡阳，10，3分）某村计划新修水渠3600米，为了让水渠尽快投入使用，实际工作效率是原计划工作效率的1.8倍，结果提前20天完成任务，若设原计划每天修水渠
米，则下面所列方程正确的是（）
A． |
B． |
C． |
D． |
（2011湖南衡阳，8，3分）如图所示，在平面直角坐标系中，菱形MNPO的顶点P坐标是（3，4），则顶点M、N的坐标分别是（）
| A．M(5，0)，N(8，4) | B．M(4，0)，N(8，4) |
| C．M(5，0)，N(7，4) | D．M(4，0)，N(7，4) |
（2011湖南衡阳，7，3分）下列说法正确的是（）
A．在一次抽奖活动中，“中奖的概率是 ”表示抽奖100次就一定会中奖 |
| B．随机抛一枚硬币，落地后正面一定朝上 |
| C．同时掷两枚均匀的骰子，朝上一面的点数和为6 |
D．在一副没有大小王的扑克牌中任意抽一张，抽到的牌是6的概率是 |
（2011湖南衡阳，4，3分）下列几个图形是国际通用的交通标志，其中不是中心对称图形的是（）
A．B．C．D．