在某市开展城乡综合治理的活动中，需要将A、B、C三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场D、E两地进行处理. 已知运往D地的数量比运往E地的数量的2倍少l0立方来．求运往D、E两地的数量各是多少立方米?
若A地运往D地
立方米(为整数)， B地运往D地30立方米. C地运往D地的数量小于A地运往D地的2倍．其余全部运往E地．且C地运往E地不超过 l2立方米．则A、C两地运往D、E两地有哪几种方案?
已知，如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D.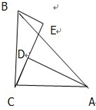
求证：△BEC≌△CDA．
先化简，再求值：[（x-y）2+（x+y）（x-y）]÷2x，其中x=3，y=—1.5 .
将下列各式分解因式：（1）x3－x；（2）－x2y＋2xy2－y3．
计算：5x（2x+1）—（2x+3）（5x—1）
如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB=14．动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．
（1）写出数轴上点B表示的数，点P表示的数（用含t的代数式表示）；
（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？
（3）若M为AP的中点，N为PB的中点．点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长；
（4）若点D是数轴上一点，点D表示的数是x，请你探索式子
是否有最小值？如果有，直接写出最小值；如果没有，说明理由．