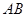 是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求:
是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示.一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求:
(1)小球运动到B点时的动能
(2)小球经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力NB、NC各是多大?
一静止的U核经一次α衰变成为一个新核,释放出的总动能为4.76 MeV.问此衰变后新核的动能为多少MeV?
半径为R的固定半圆形玻璃砖的横截面如图所示,O点为圆心,OO′为直径MN的垂线.足够大的光屏PQ紧靠在玻璃砖的右侧且与MN垂直.一束复色光沿半径方向与OO′成θ=30°角射向O点,已知复色光包含有折射率从n1=到n2=的光束,因而光屏上出现了彩色光带.
(1)求彩色光带的宽度;
(2)当复色光入射角逐渐增大时,光屏上的彩色光带将变成一个光点,求θ角至少为多少?
如图所示,质量 的木块套在水平杆上,并用轻绳与质量
的木块套在水平杆上,并用轻绳与质量 的小球相连。今用跟水平方向成30°角的力
的小球相连。今用跟水平方向成30°角的力 拉着小球带动木块一起向右匀速运动,运动中M、m相对位置保持不变,取g=10m/s2。求运动过程中轻绳与水平方向的夹角θ及木块M与水平杆间的动摩擦因数。
拉着小球带动木块一起向右匀速运动,运动中M、m相对位置保持不变,取g=10m/s2。求运动过程中轻绳与水平方向的夹角θ及木块M与水平杆间的动摩擦因数。
一质量为m =2kg的滑块能在倾角为θ=30°的足够长的斜面上以a =2.5m/s2匀加速下滑。如图所示,若用一水平推力F作用于滑块,使之由静止开始在t =2s内能沿斜面运动位移x=4m.求:(取g=10m/s2)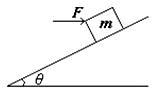
(1)滑块和斜面之间的动摩擦因数μ;
(2)推力F的大小。
某滑板爱好者在离地h=1.8m高的平台上滑行,水平离开A点后落在水平地面的B点,其水平位移X1=4.8m,(空气阻力忽略不计,g=10m/s2),求:
(1)人与滑板在空中运动的时间;
(2)人与滑板刚落地时速度的大小.