如图,AD∥FE,点B、C在AD上,∠1=∠2,BF=BC.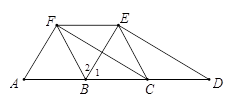
⑴ 求证:四边形BCEF是菱形
⑵ 若AB=BC=CD,求证:△ACF≌△BDE
(1)数轴上点A、点B分别是有理数-2、3对应的点,则点A、点B间的距离为.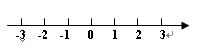
(2)再选几个点试试,猜想:若点A、点B分别是有理数a、b对应的点,则点A、点B间的距离为.
(3)若数轴上点A对应的实数为a,且|a-2|=3,则点A对应的实数为.
(4)若数轴上点A对应的实数为a,且|a-2|+|a+1|=5,则点A对应的实数为.
用字母a 表示一个有理数,则|a|一定是非负数,也就是它的值为正数或0,所以|a|的最小值为0,而-|a|一定是非正数,即它的值为负数或0,所以|a|有最大值0,根据这个结论完成下列问题:
(1)|a|+1有最值;
(2)5-|a|有最值;
(3)当a的值为时,|a-1|+2有最值;
(4)若|a-1|+|b+1|=0,则ab=.
小亮的爸爸在一家合资企业工作,月工资5500元,按规定:其中2500元是免税的,其余部分要缴纳个人所得税,应纳税部分又要分为两部分,并按不同税率纳税,即不超过1500元的部分按3%的税率;超过1500元不超过4500元的部分则按5%的税率,你能算出小亮的爸爸每月要缴纳个人所得税多少元?
上午8点,某人驾驶一辆汽车从A地出发,向东记为正,向西记为负.记录前4次行驶过程如下:-15公里,+ 25公里,-20公里,+30公里,若要汽车最后回到A地,则最后一次如何行驶?已知汽车行驶的速度为55千米/小时,在这期间他办事花去2小时,问他回到A地的时间.
计算:(1) -12+13-(9-18)
(2)
(3) 5+3×(-2)3+33
(4) 30÷(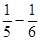 )
)