如图所示，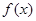
是定义在区间
（
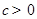）上的奇函数，令
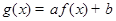，并有关于函数
的四个论断：
①若
，对于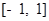
内的任意实数
（
），
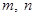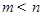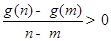恒成立；
②函数是奇函数的充要条件是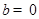
；
③若
，
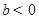，则方程
必有3个实数根；
④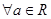
，的导函数
有两个零点；
其中所有正确结论的序号是( )．
| A．①② | B．①②③ |
| C．①④ | D．②③④ |
两条异面直线在同一平面内的射影是（）
A两条相交直线B 两条平行直线
C一条直线和不在这条直线上的一个点 D 以上位置均有可能。
下列命题，能得出直线m与平面α平行的是（）
| A．直线m与平面α内 所有直线平行 |
| B．直线m 与平面α内无数条直线平行 |
| C．直线m与平面α没有公共点 |
| D．直线m与平面α内的一条直线平行 |
空间三个平面能把空间分成的部分为（）
A 6或4 B 7或8 C 5或6或7 D 4或6或7或8
函数在[a,b]上为单调函数，则（）
| A．在[a,b]上不可能有零点 |
B．在[a,b]上若有零点，则必有 |
C．在[a,b]上若有零点，则必有 |
| D．以上都不对 |
设
，
，则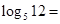
( )
A． |
B． |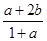
C． |
D． |