如图,在直角梯形ABCD中,AB∥DC,∠D=90o,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).求证:△ACD∽△BAC;
求DC的长;
设四边形AFEC的面积为y,求y 关于t的函数关系式,并求出y的最小值.
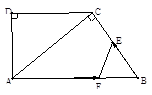
解方程:
画出几何体的三视图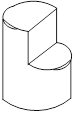
如图①,四边形ABCD是正方形,G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.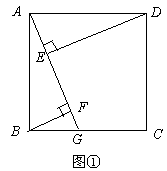
⑴求证:DE-BF=EF.
⑵当点G为BC边中点时,试探究线段EF与GF之间的数量关系,并说明理由.
⑶若点G为CB延长线上一点,其余条件不变.请你在图②中画出图形,写出此时DE、BF、EF之间的数量关系,并说明理由.
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若 ,
,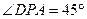

⑴求⊙O的半径;
⑵求图中阴影部分的面积
如图所示,点A坐标为(0,3),OA半径为1,点B在x轴上.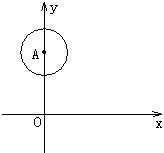
⑴若点B坐标为(4,0),⊙B半径为3,试判断⊙A与⊙B位置关系;
⑵若⊙B过M(-2,0)且与⊙A相切,求B点坐标.